Quick Tour¶
Set up¶
Interactive Rings shell¶
To taste what Rings can do, one can try interactive Rings session with Ammonite REPL. One can install Rings.repl with Homebrew:
$ brew install PoslavskySV/rings/rings.repl
or just by typing the following commands at the prompt:
$ sudo curl -L -o /usr/local/bin/amm https://git.io/v5Tct && sudo chmod +x /usr/local/bin/amm
$ sudo curl -L -o /usr/local/bin/rings.repl https://git.io/vd7EY && chmod +x /usr/local/bin/rings.repl
Now run Rings.repl:
$ rings.repl
Loading...
Rings 2.3: efficient Java/Scala library for polynomial rings
@ implicit val ring = MultivariateRing(Z, Array("x", "y", "z"))
ring: MultivariateRing[IntZ] = MultivariateRing(Z, Array("x", "y", "z"), LEX)
@ val poly1 = ring("x + y - z").pow(8)
poly1: MultivariatePolynomial[IntZ] = z^8-8*y*z^7+28*y^2*z^6-56*y^3*z^5+70*y^4*z^4-56...
@ val poly2 = ring("x - y + z").pow(8)
poly1: MultivariatePolynomial[IntZ] = z^8-8*y*z^7+28*y^2*z^6-56*y^3*z^5+70*y^4*z^4-56...
@ Factor(poly1 - poly2)
res13: FactorDecomposition[MultivariatePolynomial[IntZ]] = 16*x*(-z+y)*(z^2-2*y*z+y^2+x^2)*(z^4-4*y*z^3+6*y^2*z^2-4*y^3*z+y^4+6*x^2*z^2-12*x^2*y*z+6*x^2*y^2+x^4)
Java/Scala library¶
Rings is currently available for Java and Scala. To get started with Scala SBT, simply add the following dependence to your build.sbt file:
libraryDependencies += "cc.redberry" %% "rings.scaladsl" % "2.3"
For using Rings solely in Java there is Maven artifact:
<dependency>
<groupId>cc.redberry</groupId>
<artifactId>rings</artifactId>
<version>2.3</version>
</dependency>
Examples: rings, ideals, Gröbner bases, GCDs & factorization¶
Below examples can be evaluated directly in the Rings.repl. For Scala/Java the following preambula will import all required things from Rings library:
import cc.redberry.rings
import rings.poly.PolynomialMethods._
import rings.scaladsl._
import syntax._
import cc.redberry.rings.*;
import cc.redberry.rings.poly.*;
import cc.redberry.rings.poly.univar.*;
import cc.redberry.rings.poly.multivar.*;
import cc.redberry.rings.bigint.BigInteger;
import static cc.redberry.rings.poly.PolynomialMethods.*;
import static cc.redberry.rings.Rings.*;
Some built-in rings¶
Polynomial rings over \(Z\) and \(Q\):
// Ring Z[x]
UnivariateRing(Z, "x")
// Ring Z[x, y, z]
MultivariateRing(Z, Array("x", "y", "z"))
// Ring Q[a, b, c]
MultivariateRing(Q, Array("a", "b", "c"))
// Ring Z[x]
UnivariateRing(Z);
// Ring Z[x, y, z]
MultivariateRing(3, Z);
// Ring Q[x, y, z]
MultivariateRing(3, Q);
Polynomial rings over \(Z_p\):
// Ring Z/3[x]
UnivariateRingZp64(3, "x")
// Ring Z/3[x, y, z]
MultivariateRingZp64(3, Array("x", "y", "z"))
// Ring Z/p[x, y, z] with p = 2^107 - 1 (Mersenne prime)
MultivariateRing(Zp(Z(2).pow(107) - 1), Array("x", "y", "z"))
// Ring Z/3[x]
UnivariateRingZp64(3);
// Ring Z/3[x, y, z]
MultivariateRingZp64(3, 3);
// Ring Z/p[x, y, z] with p = 2^107 - 1 (Mersenne prime)
MultivariateRing(3, Zp(BigInteger.ONE.shiftLeft(107).decrement()));
Galois fields:
// Galois field with cardinality 7^10
// (irreducible polynomial will be generated automatically)
GF(7, 10, "x")
// GF(7^3) generated by irreducible polynomial "1 + 3*z + z^2 + z^3"
GF(UnivariateRingZp64(7, "z")("1 + 3*z + z^2 + z^3"), "z")
// Galois field with cardinality 7^10
// (irreducible polynomial will be generated automatically)
GF(7, 10);
// GF(7^3) generated by irreducible polynomial "1 + 3*z + z^2 + z^3"
GF(UnivariatePolynomialZ64.create(1, 3, 1, 1).modulus(7));
Fields of rational functions:
// Field of fractions of univariate polynomials Z[x]
Frac(UnivariateRing(Z, "x"))
// Field of fractions of multivariate polynomials Z/19[x, y, z]
Frac(MultivariateRingZp64(19, Array("x", "y", "z")))
// Field of fractions of univariate polynomials Z[a]
Frac(UnivariateRing(Z));
// Field of fractions of multivariate polynomials Z/19[a, b, c]
Frac(MultivariateRingZp64(3, 19));
Univariate polynomials¶
Some algebra in Galois field \(GF(17,9)\):
// Galois field GF(17, 9) with irreducible
// poly in Z/17[t] generated automaticaly
implicit val ring = GF(17, 9, "t")
// pick some random field element
val a = ring.randomElement()
// raise field element to the power of 1000
val b = a.pow(1000)
// reciprocal of field element
val c = 1 / b
assert ( b * c === 1)
// explicitly parse field element from string:
// input poly will be automatically converted to
// element of GF(17, 9) (reduced modulo field generator)
val d = ring("1 + t + t^2 + t^3 + 15 * t^999")
// do some arbitrary math ops in the field
val some = a / (b + c) + a.pow(6) - a * b * c * d
// Galois field GF(17, 9) with irreducible
// poly in Z/17[t] generated automaticaly
FiniteField<UnivariatePolynomialZp64> ring = GF(17, 9);
// pick some random field element
UnivariatePolynomialZp64 a = ring.randomElement();
// raise field element to the power of 1000
UnivariatePolynomialZp64 b = ring.pow(a, 1000);
// reciprocal of field element
UnivariatePolynomialZp64 c = ring.reciprocal(b);
assert ring.multiply(b, c).isOne();
// explicitly parse field element from string:
// input poly will be automatically converted to
// element of GF(17, 9) (reduced modulo field generator)
UnivariatePolynomialZp64 d = ring.parse("1 + x + x^2 + x^3 + 15*x^999");
// do some arbitrary math ops in the field
UnivariatePolynomialZp64 some = ring.add(
ring.divideExact(a, ring.add(b, c)),
ring.pow(a, 6),
ring.negate(ring.multiply(a, b, c, d)));
Extended GCD in \(Z_{17}[x]\):
// polynomial ring Z/17[x]
implicit val ring = UnivariateRingZp64(17, "x")
// parse ring element
val x = ring("x")
// construct some polynomials
val poly1 = 1 + x + x.pow(2) + x.pow(3)
val poly2 = 1 + 2 * x + 9 * x.pow(2)
// compute (gcd, s, t) such that s * poly1 + t * poly2 = gcd
val Array(gcd, s, t) = PolynomialExtendedGCD(poly1, poly2)
assert (s * poly1 + t * poly2 == gcd)
println((gcd, s, t))
// construct polynomials in Z/17[x] given by arrays of coefficients
UnivariatePolynomialZp64
a = UnivariatePolynomialZ64.create(1, 1, 1, 1).modulus(17),
b = UnivariatePolynomialZ64.create(1, 2, 9).modulus(17);
// compute xgcd array such that xgcd[1] * poly1 + xgcd[2] * poly2 = xgcd[0]
UnivariatePolynomialZp64[] xgcd = PolynomialExtendedGCD(a, b);
assert xgcd[0].equals(xgcd[1].clone().multiply(a).add(xgcd[2].clone().multiply(b)));
System.out.println(Arrays.toString(xgcd));
Factor polynomial in \(Z_{17}[x]\):
// polynomial ring Z/17[x]
implicit val ring = UnivariateRingZp64(17, "x")x
// parse polynomial from string
val poly = ring("4 + 8*x + 12*x^2 + 5*x^5 - x^6 + 10*x^7 + x^8")
// factorize poly
val factors = Factor(poly)
println(factors)
// the modulus
long modulus = 17;
// parse univariate poly over Z/17 from string
UnivariatePolynomialZp64 poly = UnivariatePolynomialZp64
.parse("4 + 8*x + 12*x^2 + 5*x^5 - x^6 + 10*x^7 + x^8", modulus);
// factorize poly
FactorDecomposition<UnivariatePolynomialZp64> factors = Factor(poly);
System.out.println(factors);
Coefficient rings with arbitrary large characteristic are available:
// coefficient ring Z/1237940039285380274899124357 (the next prime to 2^100)
val modulus = Z("1267650600228229401496703205653")
val cfRing = Zp(modulus)
// ring Z/1237940039285380274899124357[x]
implicit val ring = UnivariateRing(cfRing, "x")
val poly = ring("4 + 8*x + 12*x^2 + 5*x^5 + 16*x^6 + 27*x^7 + 18*x^8")
// factorize poly
println(Factor(poly))
// coefficient ring Z/1237940039285380274899124357 (the next prime to 2^100)
IntegersZp cfRing = Zp(new BigInteger("1267650600228229401496703205653"));
UnivariatePolynomial<BigInteger> poly = UnivariatePolynomial
.parse("4 + 8*x + 12*x^2 + 5*x^5 - x^6 + 10*x^7 + x^8", cfRing);
// factorize poly
System.out.println(Factor(poly));
(large primes can be generated with BigPrimes.nextPrime method, see Prime numbers).
Ring of univariate polynomials over elements of Galois field \(GF(7,3)[x]\):
// elements of coefficient field GF(7,3) are represented as polynomials
// over "z" modulo irreducible polynomial "1 + 3*z + z^2 + z^3"
val cfRing = GF(UnivariateRingZp64(7, "z")("1 + 3*z + z^2 + z^3"), "z")
assert(cfRing.characteristic().intValue() == 7)
assert(cfRing.cardinality().intValue() == 343)
// polynomial ring GF(7^3)[x]
implicit val ring = UnivariateRing(cfRing, "x")
// parse poly in GF(7^3)[x] from string
// coefficients of polynomials in GF(7,3)[x] are elements
// of GF(7,3) that is polynomials over "z"
val poly = ring("1 - (1 - z^3) * x^6 + (1 - 2*z) * x^33 + x^66")
// factorize poly
val factors = Factor(poly)
println(s"${ring show factors}")
// elements of coefficient field GF(7,3) are represented as polynomials
// over "z" modulo irreducible polynomial "1 + 3*z + z^2 + z^3"
FiniteField<UnivariatePolynomialZp64> cfRing
= GF(UnivariatePolynomialZ64.create(1, 3, 1, 1).modulus(7));
assert cfRing.characteristic().intValue() == 7;
assert cfRing.cardinality().intValue() == 343;
// polynomial ring GF(7^3)[x]
UnivariateRing<UnivariatePolynomial<UnivariatePolynomialZp64>>
ring = UnivariateRing(cfRing);
// parse poly in GF(7^3)[x] from string
// coefficients of polynomials in GF(7,3)[x] are elements
// of GF(7,3) that is polynomials over "z"
UnivariatePolynomial<UnivariatePolynomialZp64>
poly = ring.parse("1 - (1 - z^3) * x^6 + (1 - 2*z) * x^33 + x^66");
// factorize poly
FactorDecomposition<UnivariatePolynomial<UnivariatePolynomialZp64>> factors = Factor(poly);
System.out.println(factors);
Multivariate polynomials¶
Some math with multivariate polynomials from \(Z[x, y, z]\):
// ring Z[x, y, z]
implicit val ring = MultivariateRing(Z, Array("x", "y", "z"))
// parse some ring elements
val (x, y, z) = ring("x", "y", "z")
// construct some polynomials using different math ops
val a = (x + y + z).pow(2) - 1
val b = (x - y - z - 1).pow(2) + x + y + z - 1
val c = (a + b + 1).pow(9) - a - b - 1
// reduce c modulo a and b (multivariate division with remainder)
val (div1, div2, rem) = c /%/% (a, b)
// ring Z[x, y, z]
MultivariateRing<MultivariatePolynomial<BigInteger>> ring = MultivariateRing(3, Z);
// assign "x", "y" and "z" to variables
MultivariatePolynomial<BigInteger>
x = ring.variable(0),
y = ring.variable(1),
z = ring.variable(2);
// construct some polynomials
MultivariatePolynomial<BigInteger> a = ring.decrement(ring.pow(ring.add(x, y, z), 2));
MultivariatePolynomial<BigInteger> b = ring.add(
ring.pow(ring.add(x, ring.negate(y), ring.negate(z), ring.getNegativeOne()), 2),
x, y, z, ring.getNegativeOne());
MultivariatePolynomial<BigInteger> c = ring.add(
ring.pow(ring.add(a, b, ring.getOne()), 9),
ring.negate(a), ring.negate(b), ring.getNegativeOne());
// reduce c modulo a and b (multivariate division with remainder)
MultivariatePolynomial<BigInteger>[] divRem = MultivariateDivision.divideAndRemainder(c, a, b);
MultivariatePolynomial<BigInteger>
div1 = divRem[0],
div2 = divRem[1],
rem = divRem[2];
Multivariate GCD in \(Z[a, b, c]\):
// ring Z[a, b, c]
implicit val ring = MultivariateRing(Z, Array("a", "b", "c"))
// parse polynomials from strings
val poly1 = ring("-b-b*c-b^2+a+a*c+a^2")
val poly2 = ring("b^2+b^2*c+b^3+a*b^2+a^2+a^2*c+a^2*b+a^3")
// compute multivariate GCD
val gcd = PolynomialGCD(poly1, poly2)
assert (poly1 % gcd === 0)
assert (poly2 % gcd === 0)
println(gcd)
String[] vars = {"a", "b", "c"};
// parse polynomials from strings
MultivariatePolynomial<BigInteger>
a = MultivariatePolynomial.parse("-b-b*c-b^2+a+a*c+a^2", Z, vars),
b = MultivariatePolynomial.parse("b^2+b^2*c+b^3+a*b^2+a^2+a^2*c+a^2*b+a^3",Z, vars);
// compute multivariate GCD
MultivariatePolynomial<BigInteger> gcd = PolynomialGCD(a, b);
System.out.println(gcd);
Factor polynomial in \(Z_{2}[x, y, z]\):
// ring Z/2[x, y, z]
implicit val ring = MultivariateRingZp64(2, Array("x", "y", "z"))
val (x, y, z) = ring("x", "y", "z")
// factorize poly
val factors = Factor(1 + (1 + x + y + z).pow(2) + (x + y + z).pow(4))
println(factors)
// coefficient ring Z/2
IntegersZp64 cfRing = new IntegersZp64(2);
MultivariatePolynomialZp64
// create unit multivariate polynomial over
// 3 variables over Z/2 using LEX ordering
one = MultivariatePolynomialZp64.one(3, cfRing, MonomialOrder.LEX),
// create "x" polynomial
x = one.createMonomial(0, 1),
// create "y" polynomial
y = one.createMonomial(1, 1),
// create "z" polynomial
z = one.createMonomial(2, 1);
// (1 + x + y + z)^2
MultivariatePolynomialZp64 poly1 = one.copy().add(x, y, z);
poly1 = polyPow(poly1, 2);
// (x + y + z)^4
MultivariatePolynomialZp64 poly2 = x.copy().add(y, z);
poly2 = polyPow(poly2, 4);
// 1 + (1 + x + y + z)^2 + (x + y + z)^4
MultivariatePolynomialZp64 poly = one.copy().add(poly1, poly2);
// factorize poly
FactorDecomposition<MultivariatePolynomialZp64> factors = Factor(poly);
System.out.println(factors);
Factor polynomial in \(Z[a, b, c]\):
// ring Z[a, b, c]
implicit val ring = MultivariateRing(Z, Array("a", "b", "c"))
val (a, b, c) = ring("a", "b", "c")
// factorize poly
val factors = Factor(1 - (1 + a + b + c).pow(2) - (2 + a + b + c).pow(3))
println(ring show factors)
MultivariatePolynomial<BigInteger>
// create unit multivariate polynomial over
// 3 variables over Z using LEX ordering
one = MultivariatePolynomial.one(3, Rings.Z, MonomialOrder.LEX),
// create "a" polynomial
a = one.createMonomial(0, 1),
// create "b" polynomial
b = one.createMonomial(1, 1),
// create "c" polynomial
c = one.createMonomial(2, 1);
// (1 + a + b + c)^2
MultivariatePolynomial<BigInteger> poly1 = one.copy().add(a, b, c);
poly1 = polyPow(poly1, 2);
// (2 + a + b + c)**3
MultivariatePolynomial<BigInteger> poly2 = one.copy().multiply(2).add(a, b, c);
poly2 = polyPow(poly2, 3);
// 1 - (1 + a + b + c)^2 - (2 + a + b + c)**3
MultivariatePolynomial<BigInteger> poly = one.copy().subtract(poly1, poly2);
// factorize poly
FactorDecomposition<MultivariatePolynomial<BigInteger>> factors = Factor(poly);
System.out.println(factors);
Factor polynomial in \(Q[x, y, z]\):
// ring Q[x, y, z]
implicit val ring = MultivariateRing(Q, Array("x", "y", "z"))
// parse some poly from string
val poly = ring(
"""
|(1/6)*y*z + (1/6)*y^3*z^2 - (1/2)*y^6*z^5 - (1/2)*y^8*z^6
|-(1/3)*x*z - (1/3)*x*y^2*z^2 + x*y^5*z^5 + x*y^7*z^6
|+(1/9)*x^2*y^2*z - (1/3)*x^2*y^7*z^5 - (2/9)*x^3*y*z
|+(2/3)*x^3*y^6*z^5 - (1/2)*x^6*y - (1/2)*x^6*y^3*z
|+x^7 + x^7*y^2*z - (1/3)*x^8*y^2 + (2/3)*x^9*y
""".stripMargin)
// factorize poly
val factors = Factor(poly)
println(factors)
// parse some poly from string
MultivariatePolynomial<Rational<BigInteger>>
poly = MultivariatePolynomial.parse(
"(1/6)*y*z + (1/6)*y^3*z^2 - (1/2)*y^6*z^5 - (1/2)*y^8*z^6" +
"-(1/3)*x*z - (1/3)*x*y^2*z^2 + x*y^5*z^5 + x*y^7*z^6" +
"+(1/9)*x^2*y^2*z - (1/3)*x^2*y^7*z^5 - (2/9)*x^3*y*z" +
"+(2/3)*x^3*y^6*z^5 - (1/2)*x^6*y - (1/2)*x^6*y^3*z" +
"+x^7 + x^7*y^2*z - (1/3)*x^8*y^2 + (2/3)*x^9*y"
, Q);
// factorize poly
System.out.println(Factor(poly));
Ring of multivariate polynomials over elements of Galois field \(GF(7,3)[x, y, z]\):
// elements of GF(7,3) are represented as polynomials
// over "z" modulo irreducible polynomial "1 + 3*z + z^2 + z^3"
val cfRing = GF(UnivariateRingZp64(7, "z")("1 + 3*z + z^2 + z^3"), "z")
// ring GF(7,3)[a,b,c]
implicit val ring = MultivariateRing(cfRing, Array("a", "b", "c"))
// parse poly in GF(7^3)[a,b,c] from string
// coefficients of polynomials in GF(7,3)[a,b,c] are elements
// of GF(7,3) that is polynomials over "z"
val poly = ring("1 - (1 - z^3) * a^6*b + (1 - 2*z) * c^33 + a^66")
//factorize poly
println(Factor(poly))
// elements of GF(7,3) are represented as polynomials
// over "z" modulo irreducible polynomial "1 + 3*z + z^2 + z^3"
FiniteField<UnivariatePolynomialZp64> cfRing
= GF(UnivariatePolynomialZ64.create(1, 3, 1, 1).modulus(7));
assert cfRing.characteristic().intValue() == 7;
assert cfRing.cardinality().intValue() == 343;
// ring GF(7,3)[a, b, c]
MultivariateRing<MultivariatePolynomial<UnivariatePolynomialZp64>>
ring = MultivariateRing(3, cfRing);
// parse poly in GF(7^3)[a,b,c] from string
// coefficients of polynomials in GF(7,3)[a,b,c] are elements
// of GF(7,3) that is polynomials over "z"
MultivariatePolynomial<UnivariatePolynomialZp64>
poly = ring.parse("1 - (1 - z^3) * a^6*b + (1 - 2*z) * c^33 + a^66");
//factorize poly
System.out.println(Factor(poly));
Ideals and Gröbner bases¶
Construct some ideal and check its properties:
// ring Z/17[x,y,z]
implicit val ring = MultivariateRingZp64(17, Array("x", "y", "z"))
val (x, y, z) = ring("x", "y", "z")
// create ideal with two generators using GREVLEX monomial order for underlying Groebner basis
val I = Ideal(ring, Seq(x.pow(2) + y.pow(12) - z, x.pow(2) * z + y.pow(2) - 1), GREVLEX)
// I is proper ideal
assert(I.isProper)
// get computed Groebner basis
val gb = I.groebnerBasis
println(gb)
// check some ideal properties
assert(I.dimension == 1)
assert(I.degree == 36)
MultivariateRing<MultivariatePolynomialZp64> ring = MultivariateRingZp64(3, 17);
// create ideal with two generators using GREVLEX monomial order for underlying Groebner basis
Ideal<MonomialZp64, MultivariatePolynomialZp64> I = Ideal.create(Arrays.asList(
ring.parse("x^2 + y^12 - z"),
ring.parse("x^2 * z + y^2 - 1")), GREVLEX);
// I is proper ideal
assert I.isProper();
// get computed Groebner basis
List<MultivariatePolynomialZp64> gb = I.getGroebnerBasis();
System.out.println(gb);
// check some ideal properties
assert I.dimension() == 1;
assert I.degree() == 36;
Unions, intersections and quotients of ideals:
// create another ideal with only one generator
val J = Ideal(ring, Seq(x.pow(4) * y.pow(4) + 1), GREVLEX)
// J is principal ideal
assert(J.isPrincipal)
val union = I union J
// union is zero dimensional ideal
assert(union.dimension == 0)
val intersection = I intersection J
// intersection is still 2-dimensional
assert(intersection.dimension == 2)
// yet another ideal
val K = Ideal(ring, Seq(z * x.pow(4) - z * y.pow(14) + y * z.pow(16), (x + y + z).pow(4)), GREVLEX)
// compute complicated quotient ideal
val quot = (I * J * K) :/ times
assert(quot == K)
// create another ideal with only one generator
Ideal<MonomialZp64, MultivariatePolynomialZp64> J = Ideal.create(Arrays.asList(
ring.parse("x^4 * y^4 + 1")), GREVLEX);
// J is principal ideal
assert J.isPrincipal();
Ideal<MonomialZp64, MultivariatePolynomialZp64> union = I.union(J);
// union is zero dimensional ideal
assert union.dimension() == 0;
Ideal<MonomialZp64, MultivariatePolynomialZp64> intersection = I.intersection(J);
// intersection is still 2-dimensional
assert intersection.dimension() == 2;
// yet another ideal
Ideal<MonomialZp64, MultivariatePolynomialZp64> K = Ideal.create(Arrays.asList(
ring.parse("z * x^4 - z * y^14 + y * z^16"),
ring.pow(ring.parse("x + y + z"), 4)), GREVLEX);
// compute complicated quotient ideal
Ideal<MonomialZp64, MultivariatePolynomialZp64> quot = (I.multiply(J).multiply(K)).quotient(times);
assert quot.equals(K);
Construct lexicographic Gröbner basis to solve a system of equations:
// ring Q[a, b, c]
implicit val ring = MultivariateRing(Q, Array("x", "y", "z"))
// parse some polynomials from strings
val a = ring("8*x^2*y^2 + 5*x*y^3 + 3*x^3*z + x^2*y*z")
val b = ring("x^5 + 2*y^3*z^2 + 13*y^2*z^3 + 5*y*z^4")
val c = ring("8*x^3 + 12*y^3 + x*z^2 + 3")
val d = ring("7*x^2*y^4 + 18*x*y^3*z^2 + y^3*z^3")
// construct ideal with Groebner basis in LEX order
val ideal = Ideal(ring, Seq(a, b, c, d), LEX)
// it is very simple: <z^2, x, 1+4*y^3>
println(ideal)
String[] vars = {"x", "y", "z"};
// parse some polynomials from strings
MultivariatePolynomial<BigInteger>
a = parse("8*x^2*y^2 + 5*x*y^3 + 3*x^3*z + x^2*y*z", Z, vars),
b = parse("x^5 + 2*y^3*z^2 + 13*y^2*z^3 + 5*y*z^4", Z, vars),
c = parse("8*x^3 + 12*y^3 + x*z^2 + 3", Z, vars),
d = parse("7*x^2*y^4 + 18*x*y^3*z^2 + y^3*z^3", Z, vars);
List<MultivariatePolynomial<BigInteger>> gens = Arrays.asList(a, b, c, d);
// construct ideal with Groebner basis in LEX order
Ideal<Monomial<BigInteger>, MultivariatePolynomial<BigInteger>> gb = Ideal.create(gens, LEX);
// Groebner bases is very simple: <x, z^2, 1 + 4*y^3>
System.out.println(gb);
Programming¶
Implement generic function for solving linear Diophantine equations:
/**
* Solves equation \sum f_i s_i = gcd(f_1, \dots, f_N) for given f_i and unknown s_i
* @return a tuple (gcd, solution)
*/
def solveDiophantine[E](fi: Seq[E])(implicit ring: Ring[E]) =
fi.foldLeft((ring(0), Seq.empty[E])) { case ((gcd, seq), f) =>
val xgcd = ring.extendedGCD(gcd, f)
(xgcd(0), seq.map(_ * xgcd(1)) :+ xgcd(2))
}
Implement generic function for computing partial fraction decomposition:
/** Computes partial fraction decomposition of given rational */
def apart[E](frac: Rational[E]) = {
implicit val ring: Ring[E] = frac.ring
val factors = ring.factor(frac.denominator).map {case (f, exp) => f.pow(exp)}
val (gcd, nums) = solveDiophantine(factors.map(frac.denominator / _))
val (ints, rats) = (nums zip factors)
.map { case (num, den) => Rational(frac.numerator * num, den * gcd) }
.flatMap(_.normal) // extract integral parts from fractions
.partition(_.isIntegral) // separate integrals and fractions
rats :+ ints.foldLeft(Rational(ring(0)))(_ + _)
}
Apply that function to elements of different rings:
// partial fraction decomposition for rationals
// gives List(184/479, (-10)/13, 1/8, (-10)/47, 1)
val qFracs = apart( Q("1234213 / 2341352"))
// partial fraction decomposition for rational functions
val ufRing = Frac(UnivariateRingZp64(17, "x"))
// gives List(4/(16+x), 1/(10+x), 15/(1+x), (14*x)/(15+7*x+x^2))
val pFracs = apart( ufRing("1 / (3 - 3*x^2 - x^3 + x^5)") )
Implement Lagrange method for univariate interpolation:
/** Lagrange polynomial interpolation formula */
def interpolate[Poly <: IUnivariatePolynomial[Poly], Coef]
(points: Seq[(Coef, Coef)])
(implicit ring: IUnivariateRing[Poly, Coef]) = {
// implicit coefficient ring (setups algebraic operators on type Coef)
implicit val cfRing: Ring[Coef] = ring.cfRing
if (!cfRing.isField) throw new IllegalArgumentException
points.indices
.foldLeft(ring(0)) { case (sum, i) =>
sum + points.indices
.filter(_ != i)
.foldLeft(ring(points(i)._2)) { case (product, j) =>
product * (ring.`x` - points(j)._1) / (points(i)._1 - points(j)._1)
}
}
}
Interpolate polynomial from \(Frac(Z_{13}[a,b,c])[x]\):
// coefficient ring Frac(Z/13[a,b,c])
val cfRing = Frac(MultivariateRingZp64(2, Array("a", "b", "c")))
val (a, b, c) = cfRing("a", "b", "c")
implicit val ring = UnivariateRing(cfRing, "x")
// interpolate with Lagrange formula
val data = Seq(a -> b, b -> c, c -> a)
val poly = interpolate(data)
assert(data.forall { case (p, v) => poly.eval(p) == v })
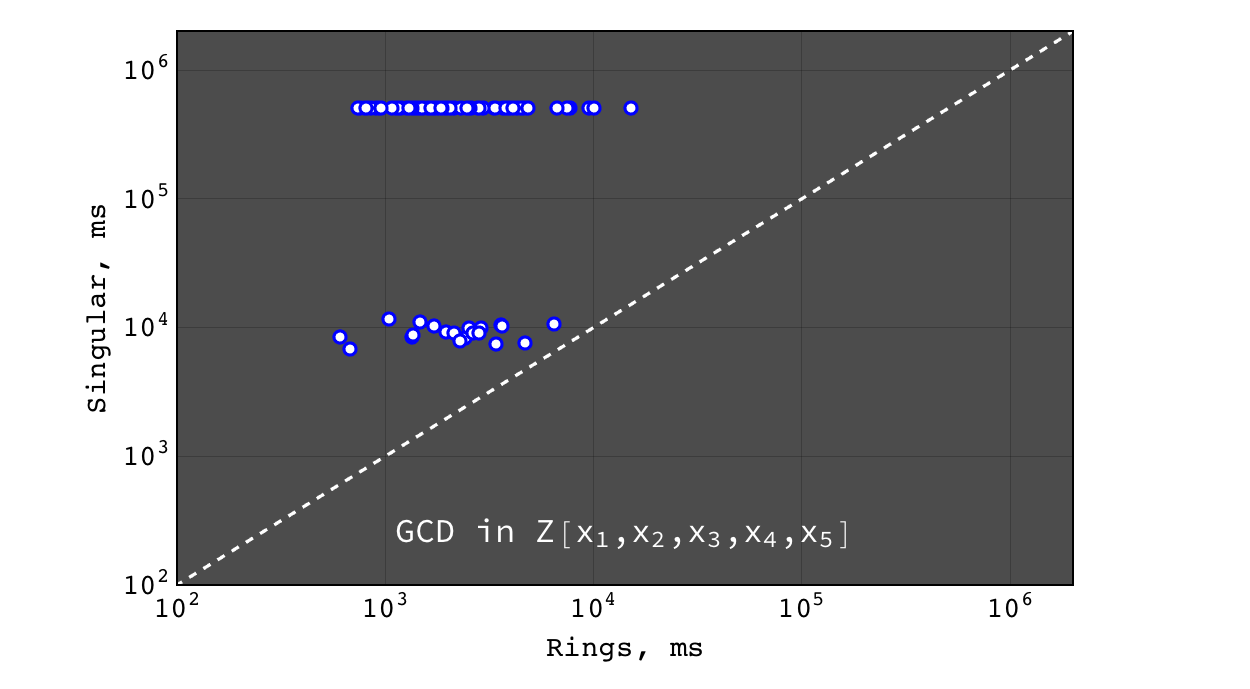
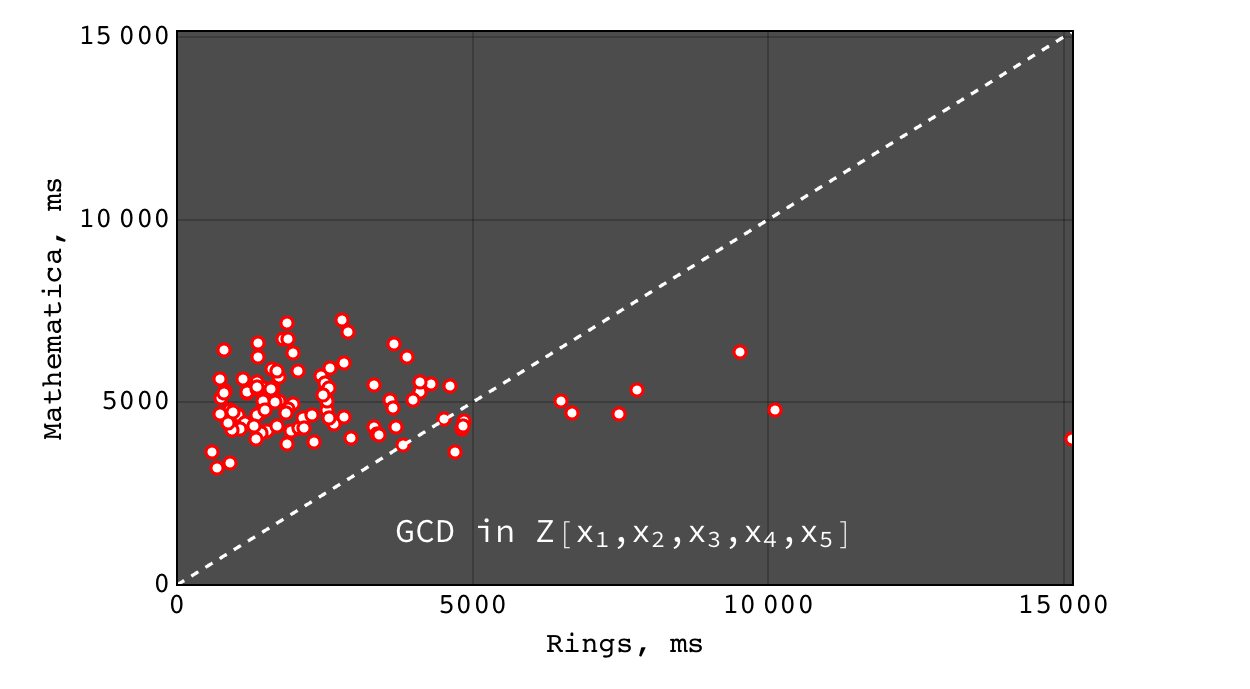
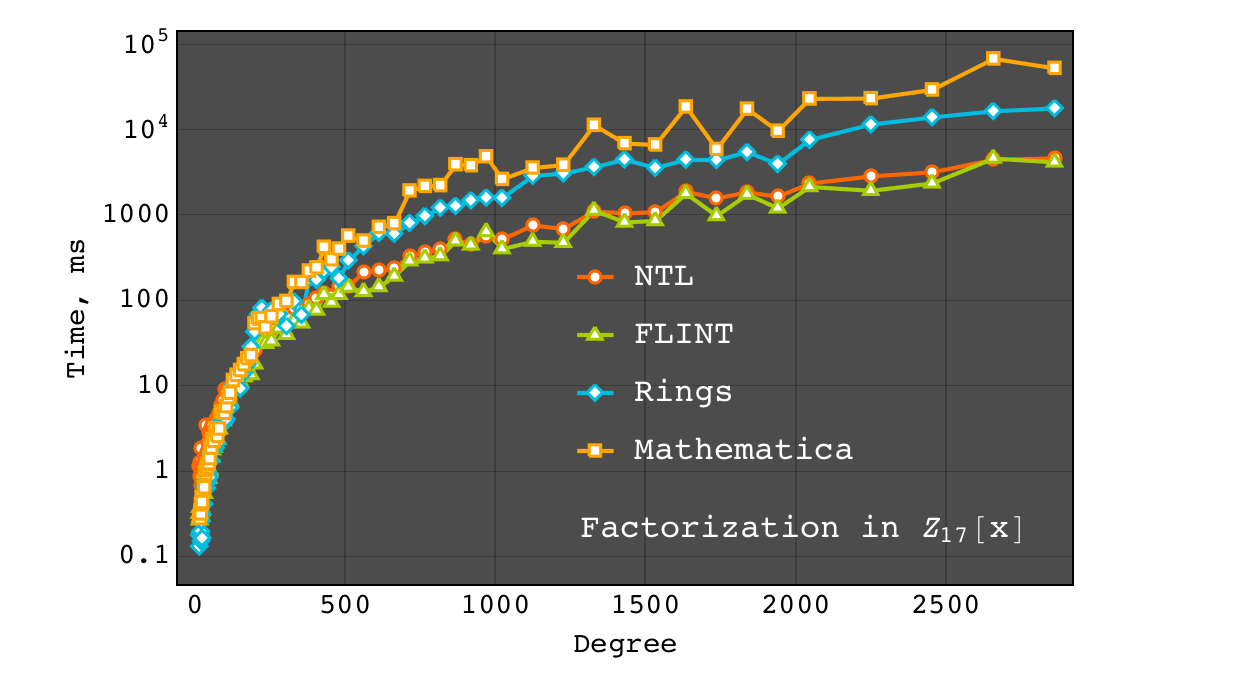
Highlighted benchmarks¶
Full benchmarks can be found at Benchmarks page. Benchmarks presented below were executed on MacBook Pro (15-inch, 2017), 3,1 GHz Intel Core i7, 16 GB 2133 MHz LPDDR3. The complete source code of benchmarks can be found at GitHub. The following software were used:
- Mathematica (version 11.1.1.0)
- Singular (version 4.1.0)
- NTL (version 10.4.0)
- FLINT (version 2.5.2_1)