Benchmarks¶
Warning
The actual benchmarks are moved to https://github.com/PoslavskySV/rings.benchmarks. Below information is outdated.
All benchmarks presented below were executed on MacBook Pro (15-inch, 2017), 3,1 GHz Intel Core i7, 16 GB 2133 MHz LPDDR3. The complete source code of benchmarks can be found at GitHub. The following software were used:
- Mathematica (version 11.1.1.0)
- Singular (version 4.1.0)
- NTL (version 10.4.0)
- FLINT (version 2.5.2_1)
Multivariate GCD¶
Multivariate GCD performance was tested on random polynomials in the following way. Polynomials \(a\), \(b\) and \(g\) with 40 terms and degree 20 in each variable were generated at random. Then the GCDs \(gcd(a g, b g)\) (should result in multiple of \(g\)) and \(gcd(a g + 1, b g)\) (usually 1) were calculated. So the input polynomials had about ~1000 terms and degree 40 in each variable (so the total degree of input was \(40 * n\), where \(n\) is the number of variables). Tests were performed for polynomials in 3, 4 and 5 variables over \(Z\) and \(Z_2\) ground rings.
Brief conclusion
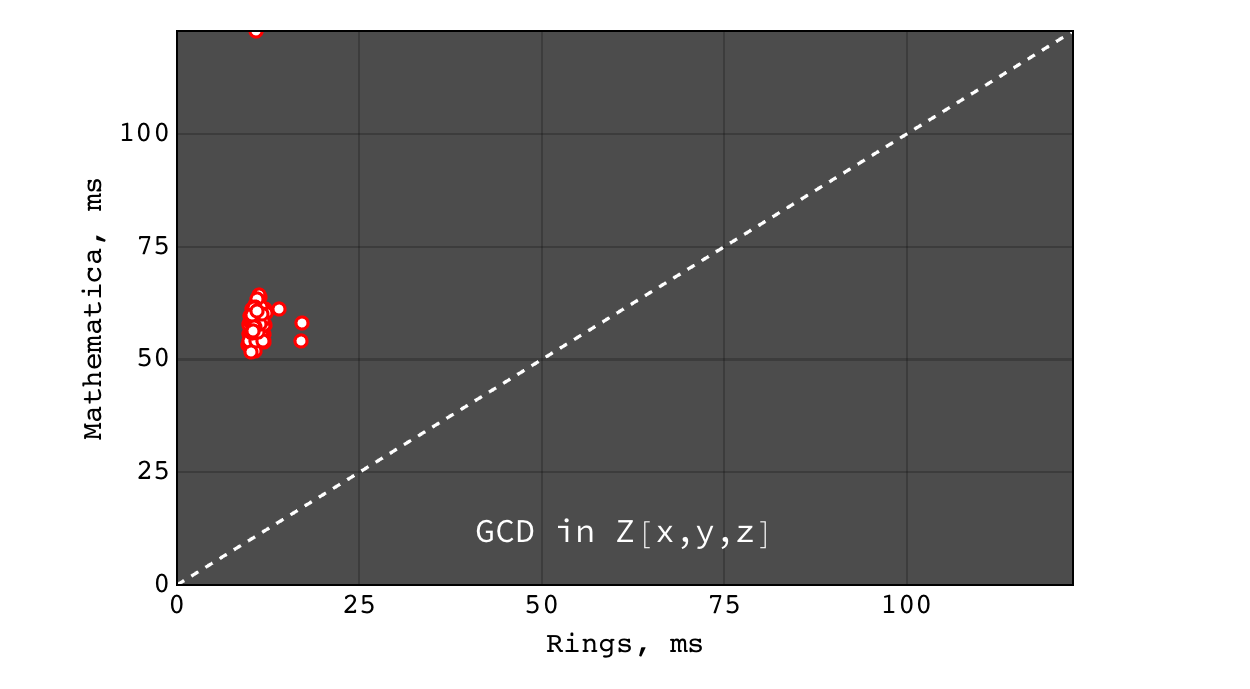
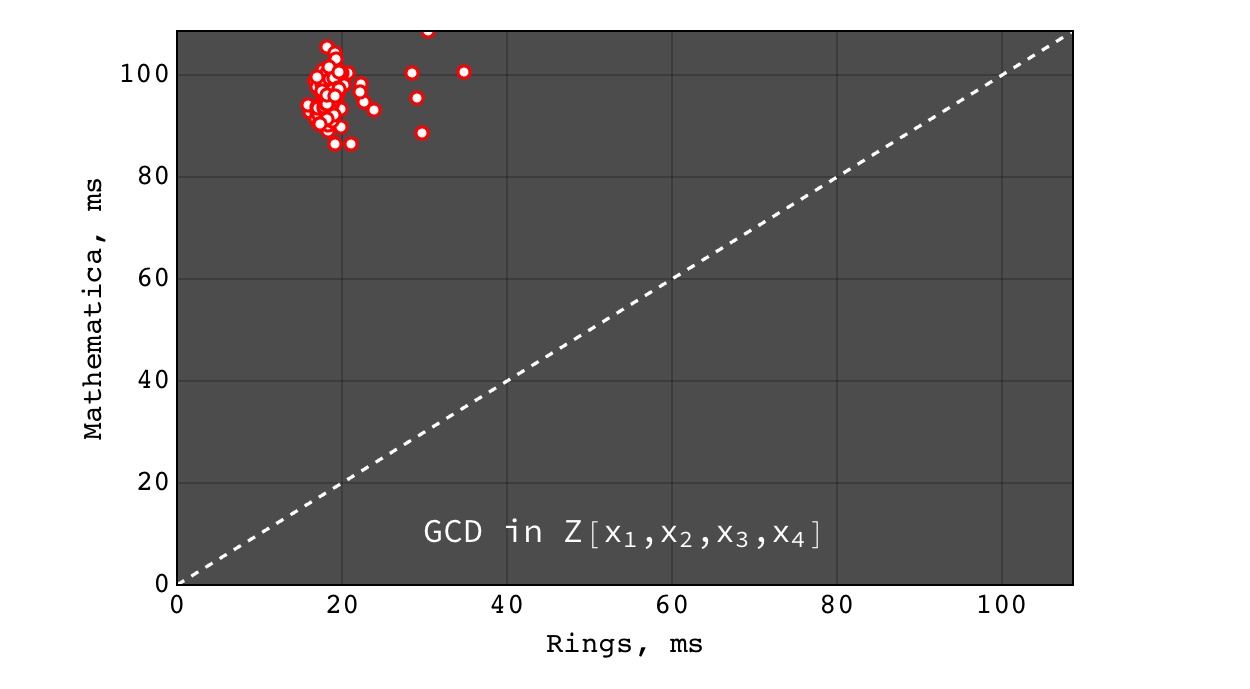
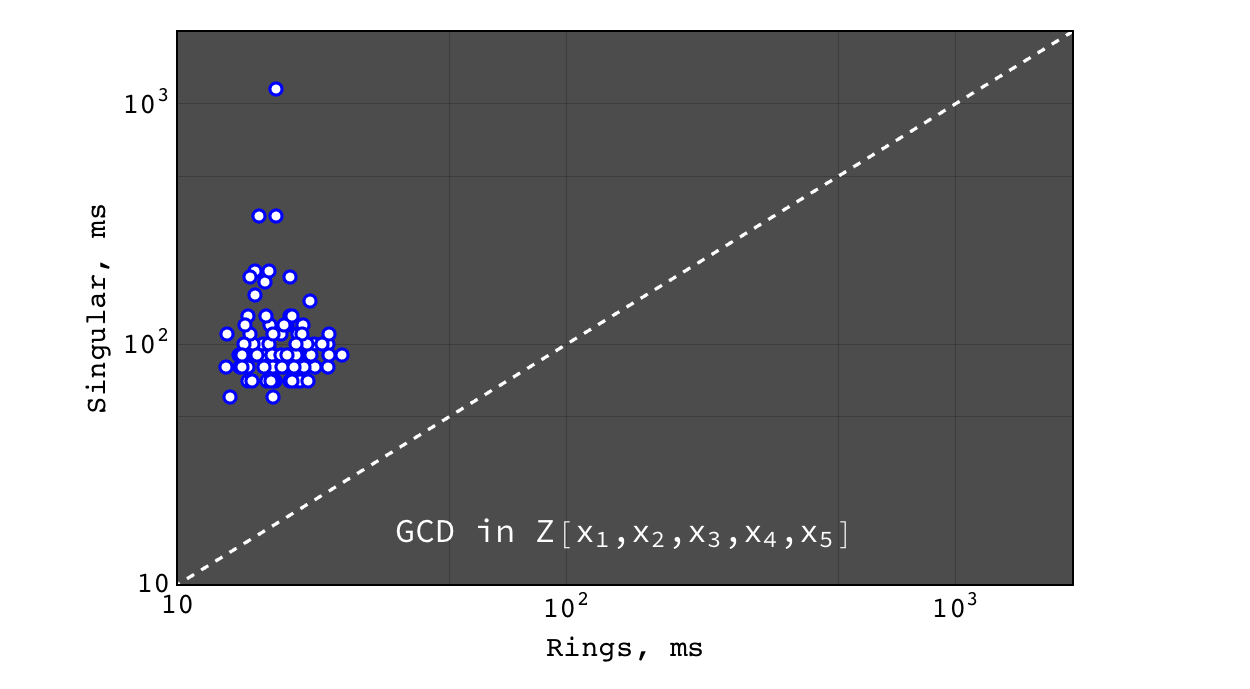
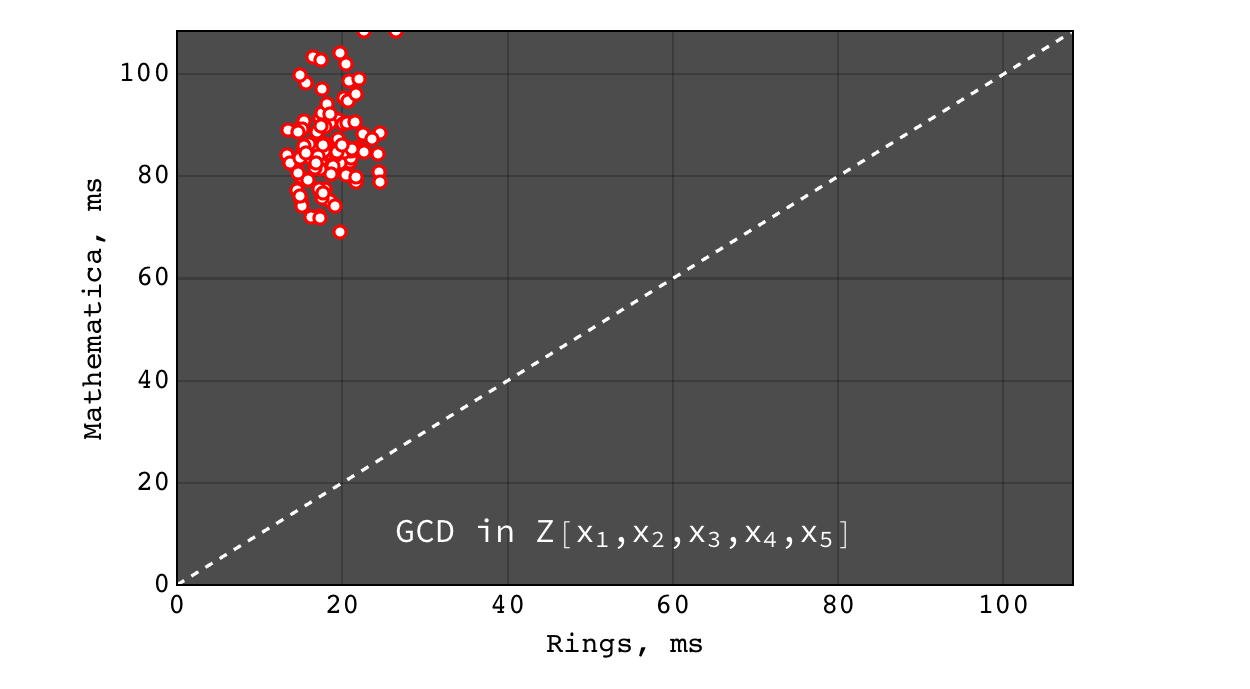
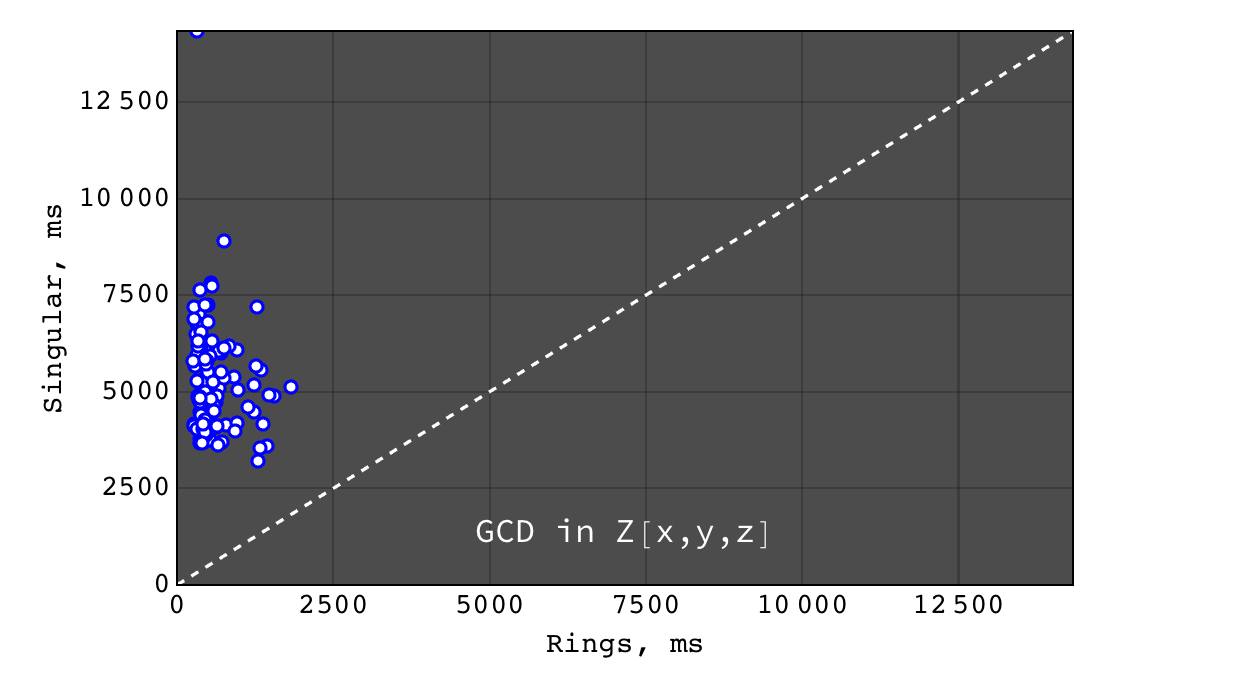
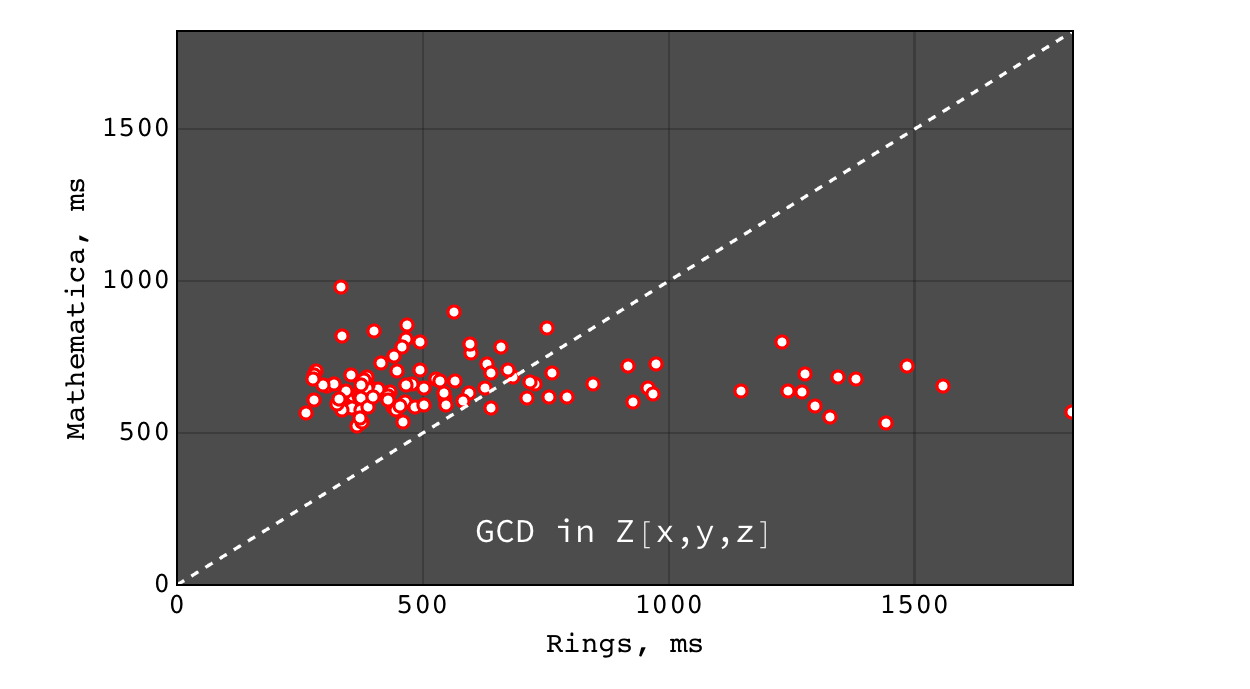
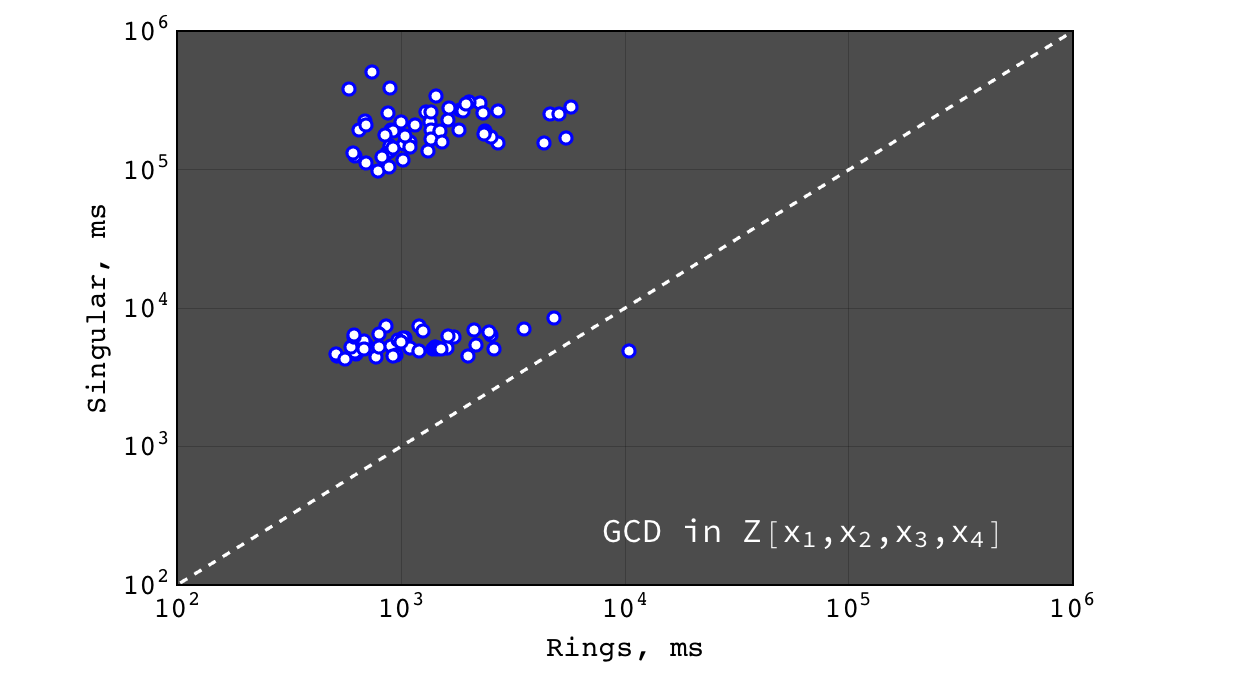
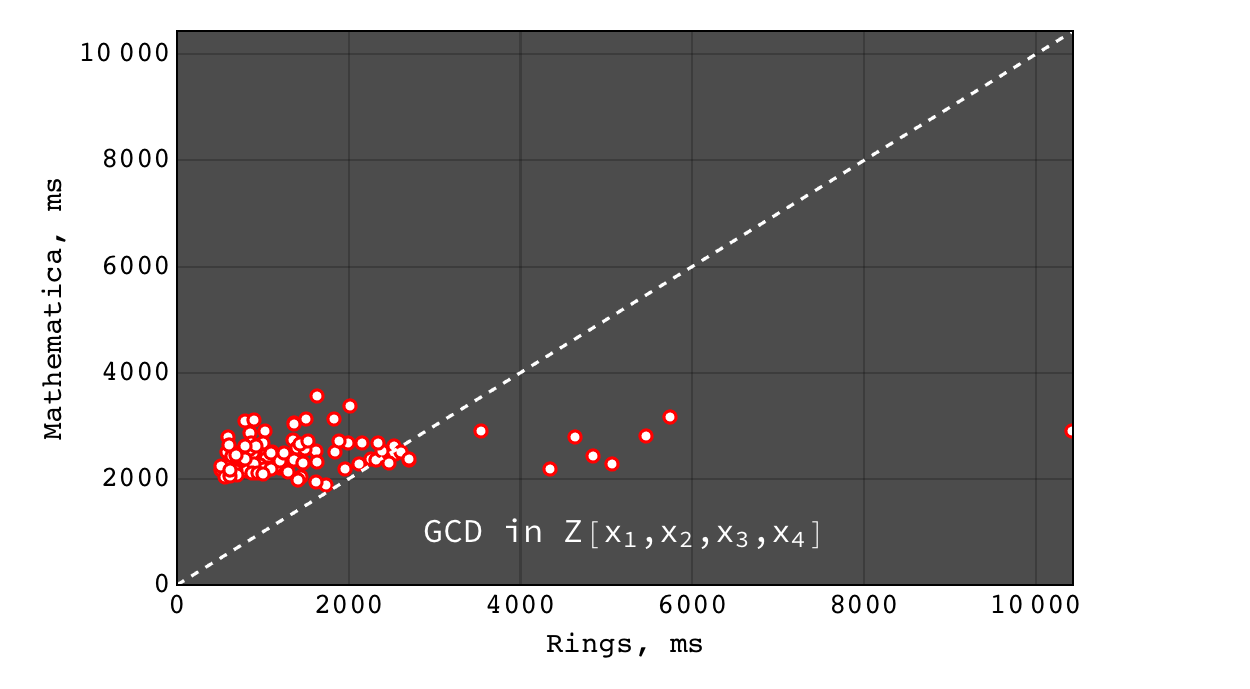
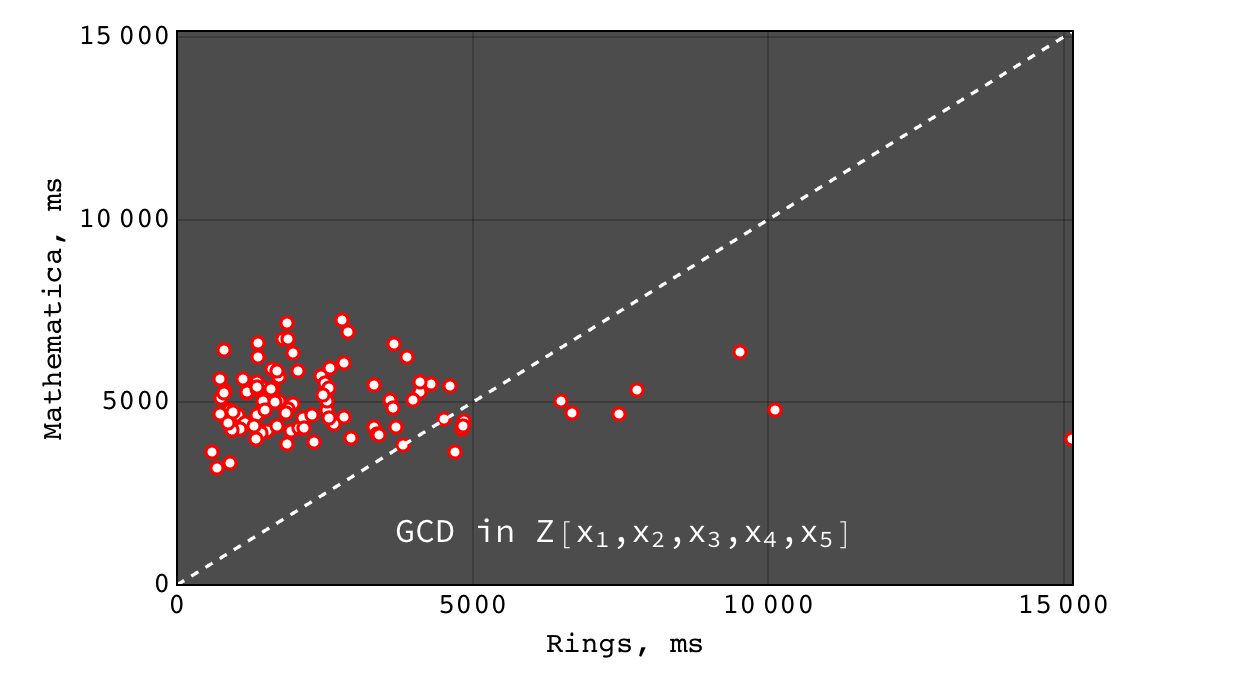
- for non trivial GCD problems Rings are several orders of magnitude faster than Singular (on polynomials over all domains) and Mathematica (on polynomials over finite fields) and slightly faster than Mathematica for polynomials over Z
- for a relatively prime polynomials, all tools show comparable (very good) performace
Multivariate GCD over \(Z_2\)¶
Mathematica failed to solve GCD problem for medium-sized polynomials considered in this benchmark in most cases in a reasonable time (minutes), so in this benchmark we compared only Rings and Singular.
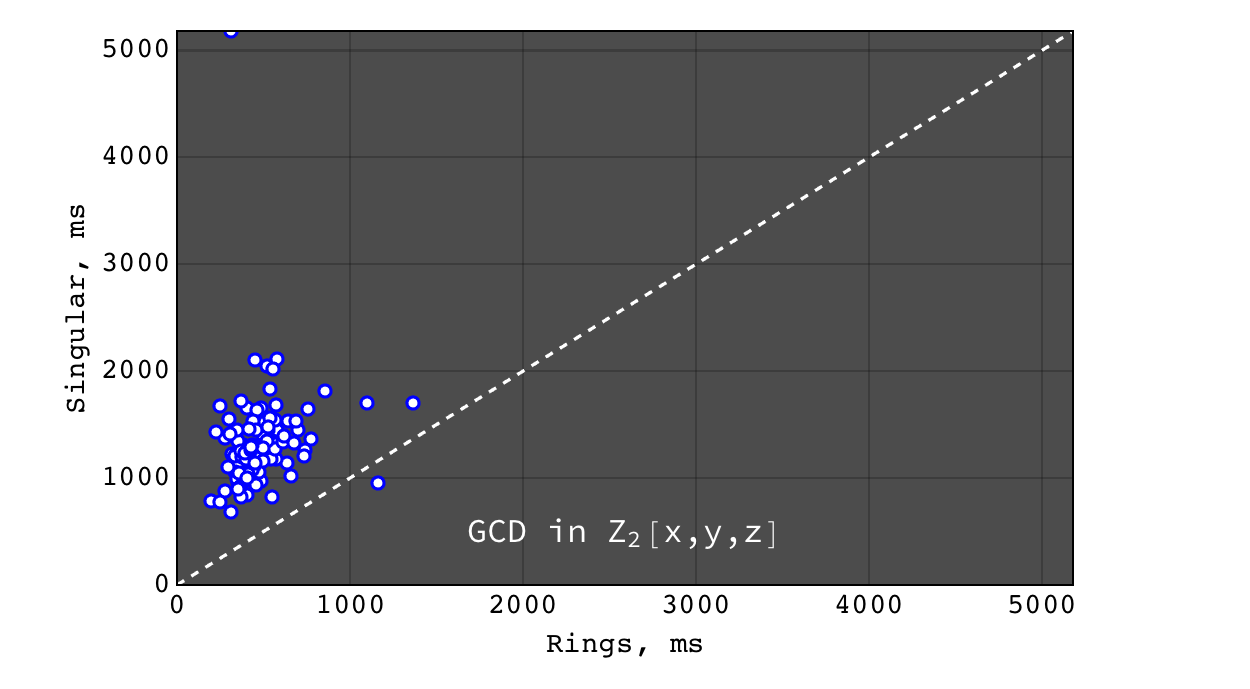
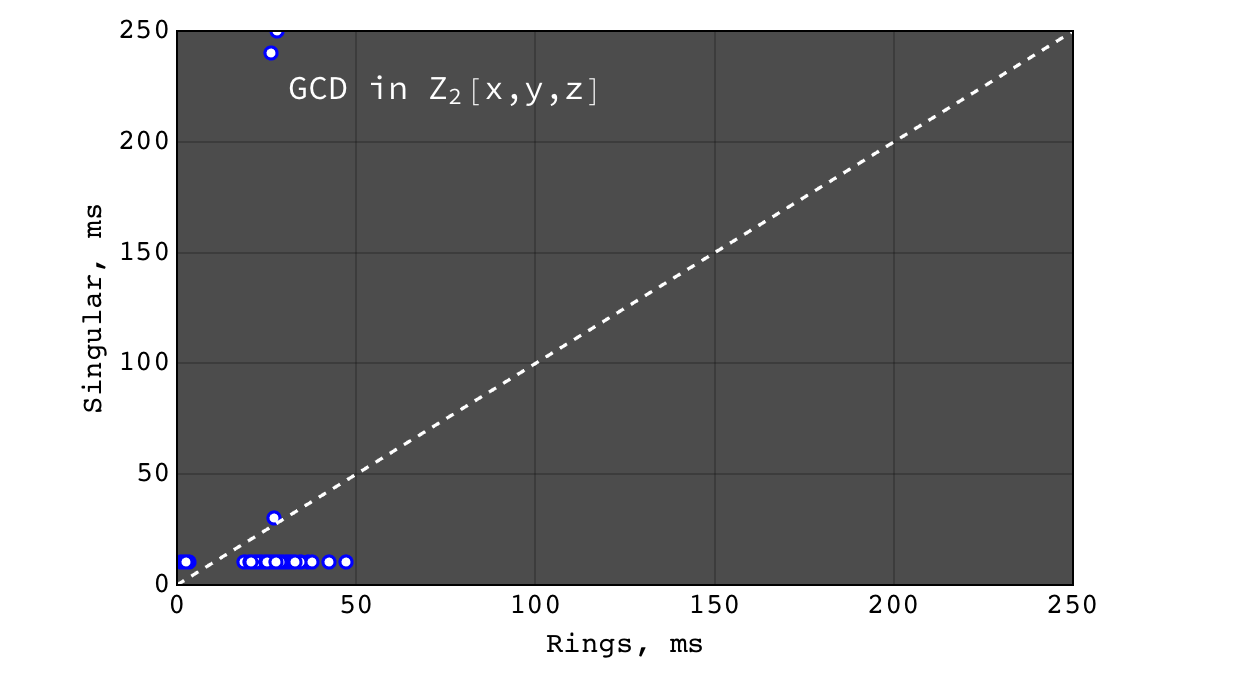
GCD in \(Z_2[x,y,z]\)¶
Performance of GCD in \(Z_2[x,y,z]\)
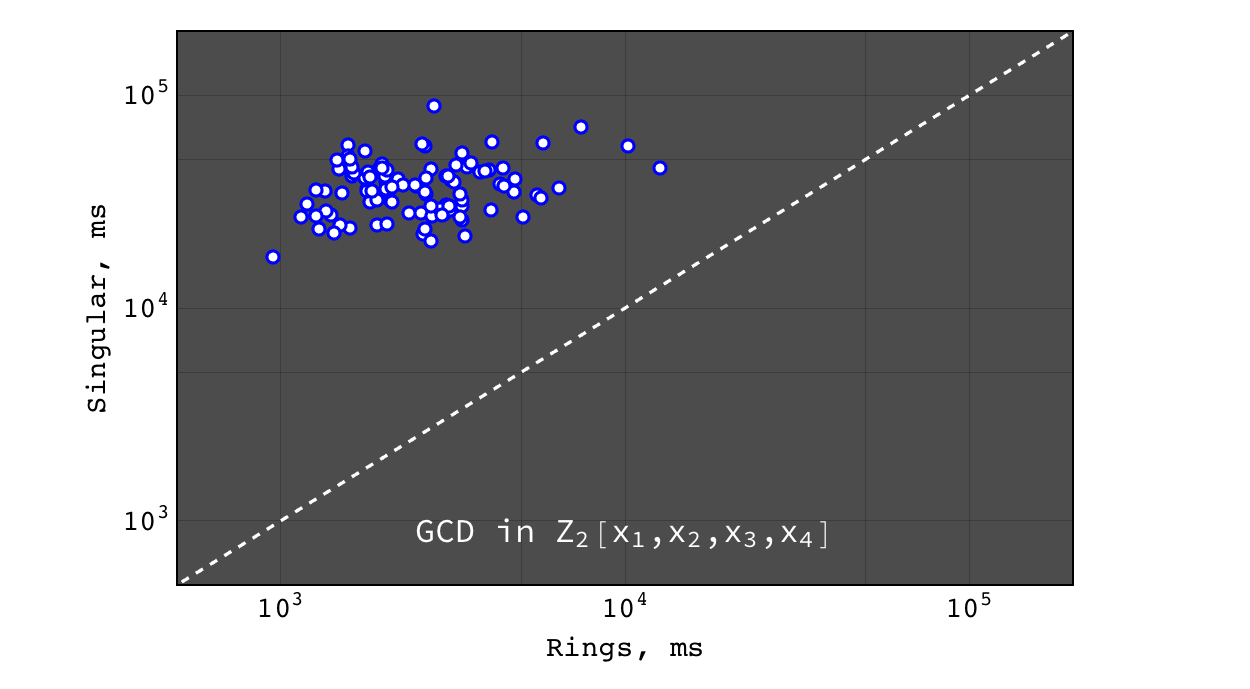
GCD in \(Z_2[x_1,x_2,x_3,x_4]\)¶
Performance of GCD in \(Z_2[x_1,x_2,x_3,x_4]\)
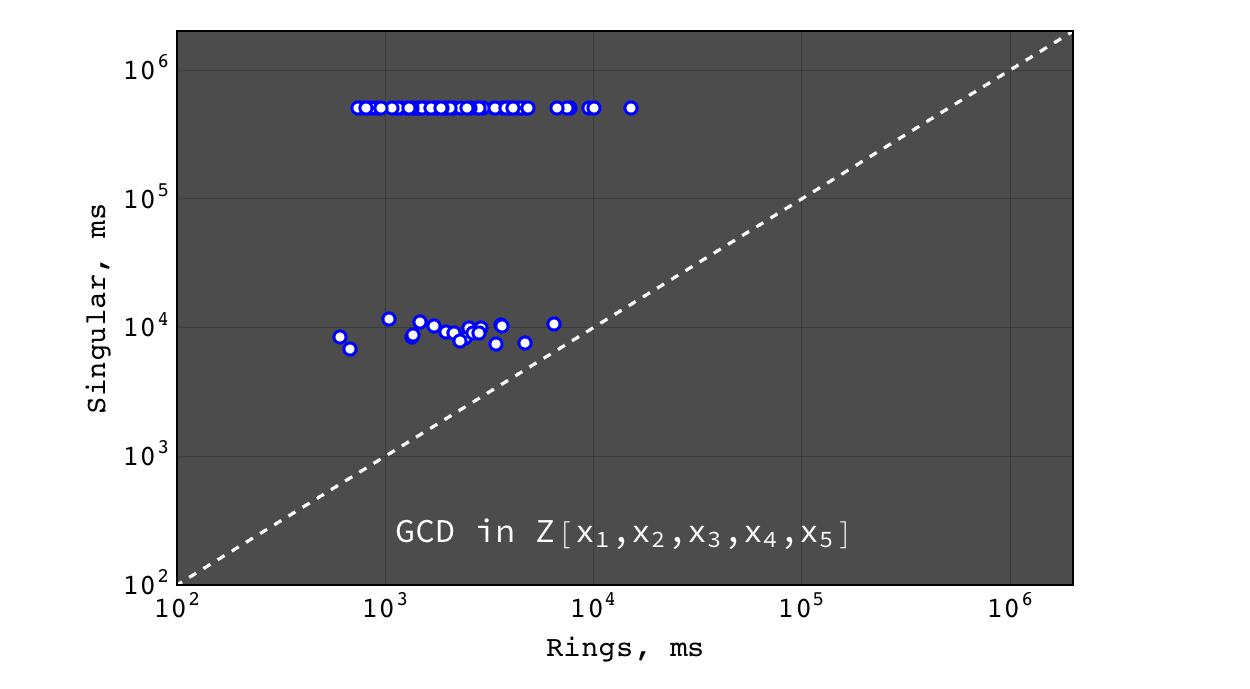
GCD in \(Z_2[x_1,x_2,x_3,x_4, x_5]\)¶
In all these tests Singular failed to obtain result within 500 seconds, while Rings calculated GCD within less than 5 seconds.
Multivariate GCD over \(Z\)¶
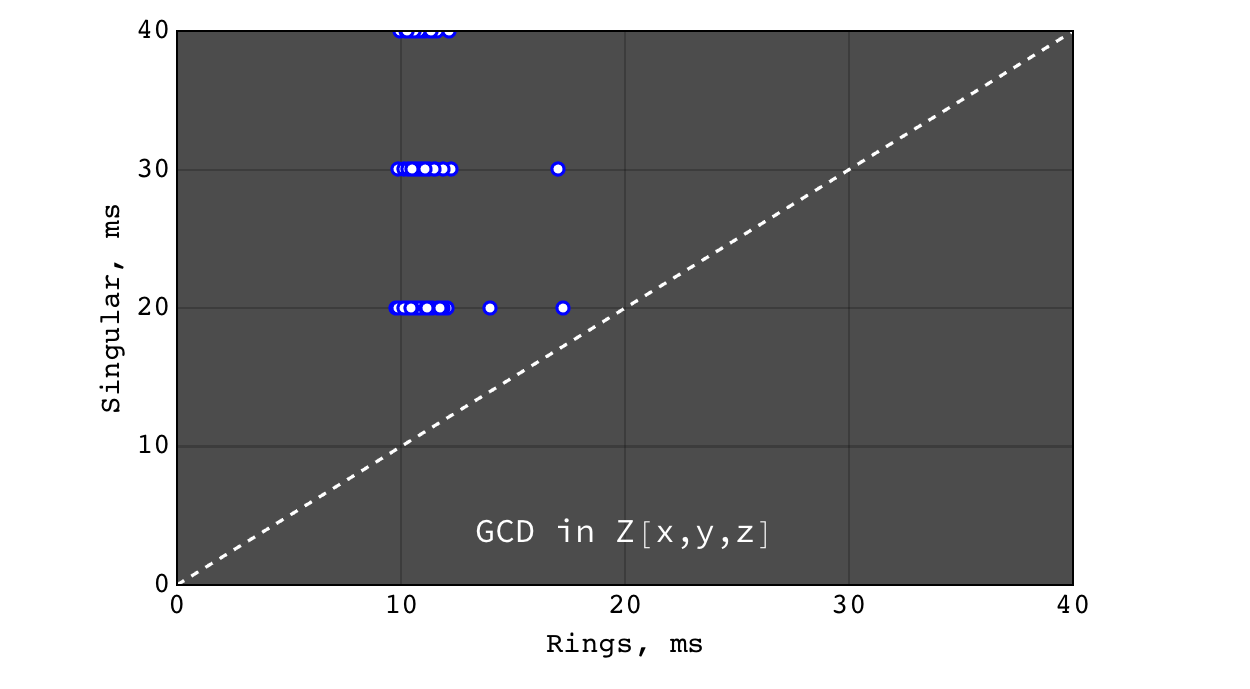
GCD in \(Z[x,y,z]\)¶
GCD in \(Z[x_1,x_2,x_3,x_4]\)¶
GCD in \(Z[x_1,x_2,x_3,x_4,x_5]\)¶
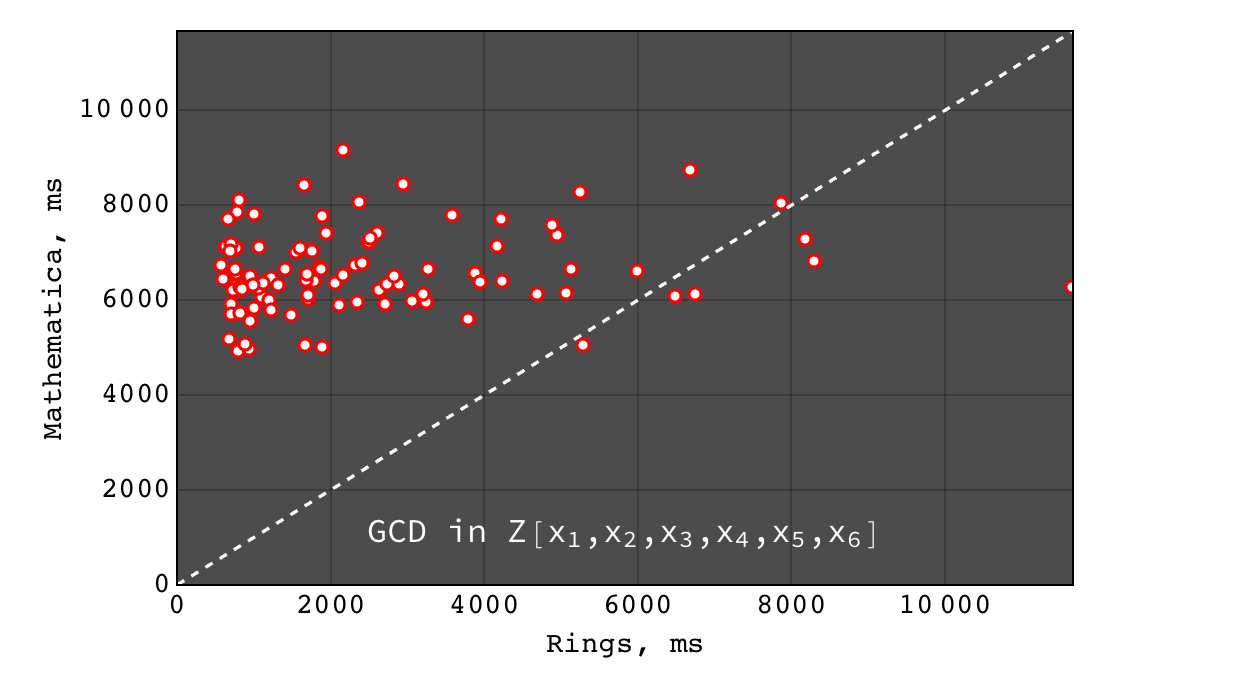
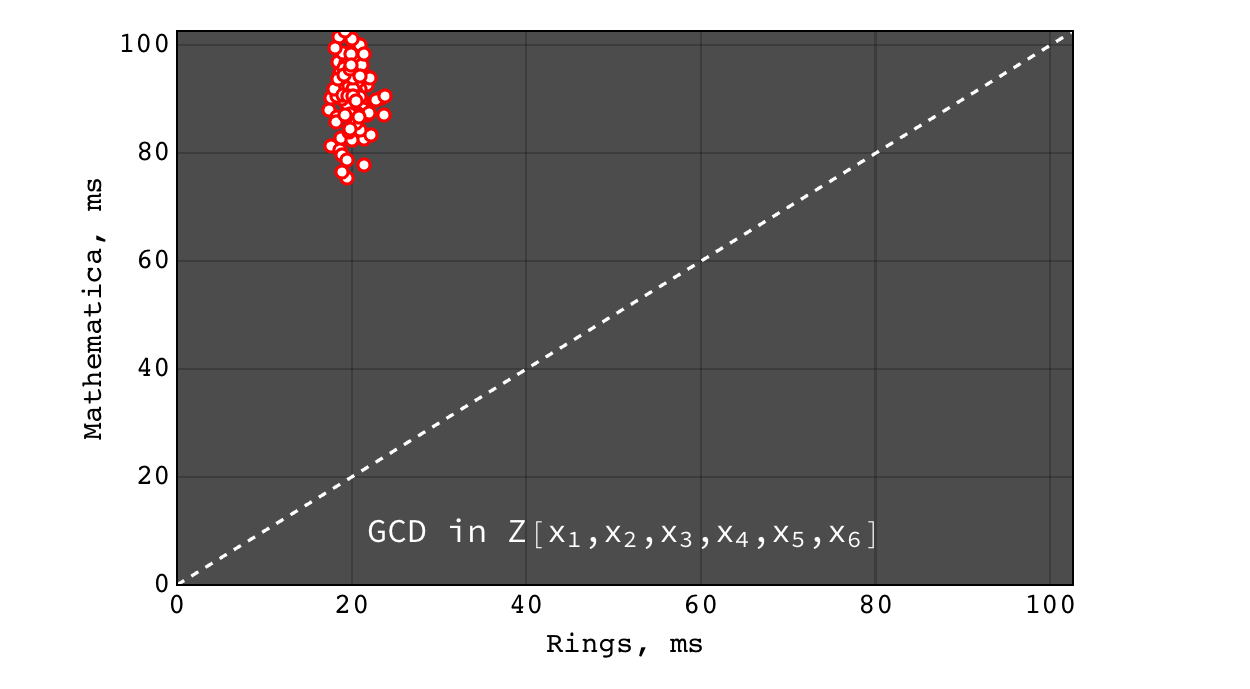
GCD in \(Z[x_1,x_2,x_3,x_4,x_5,x_6]\)¶
In all these tests Singular failed to obtain result within 500 seconds, so we present only Rings vs Mathematica comparison.
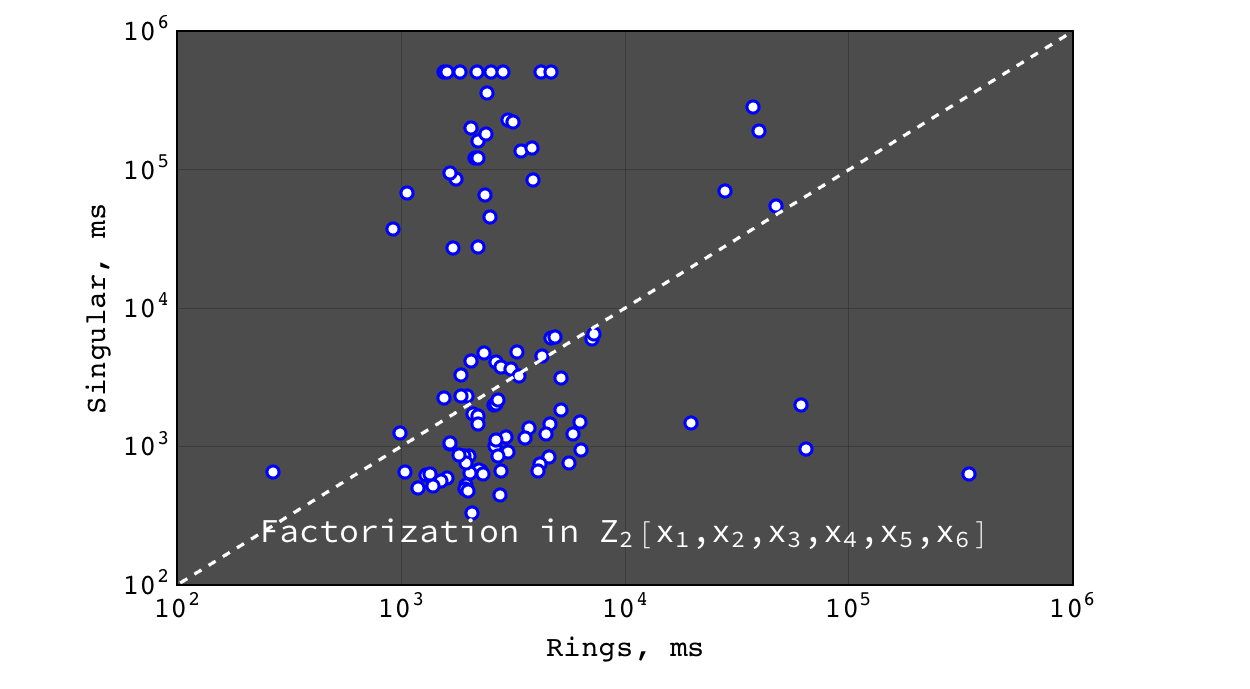
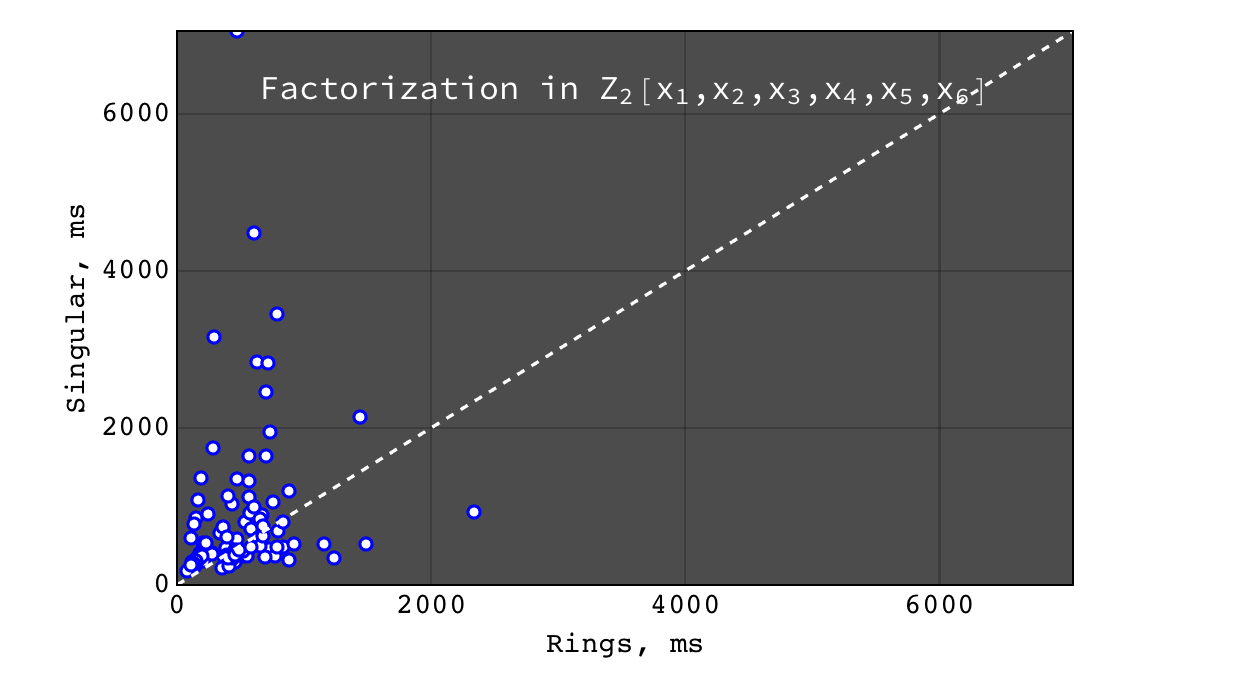
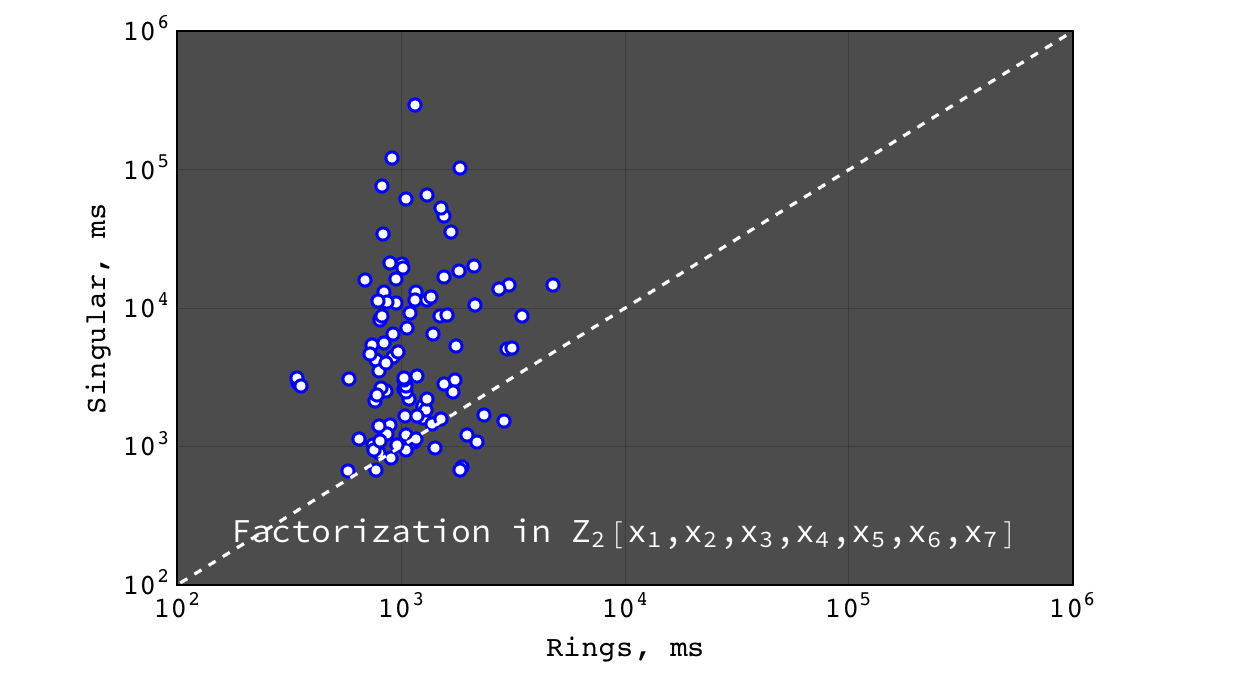
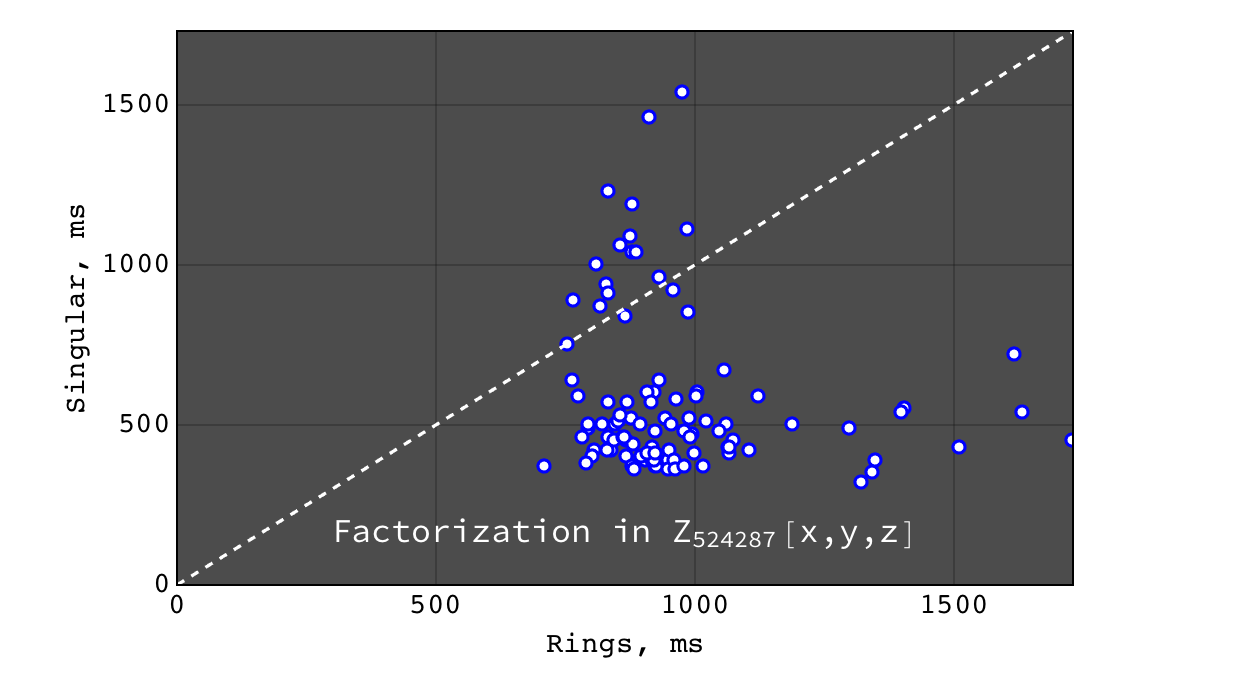
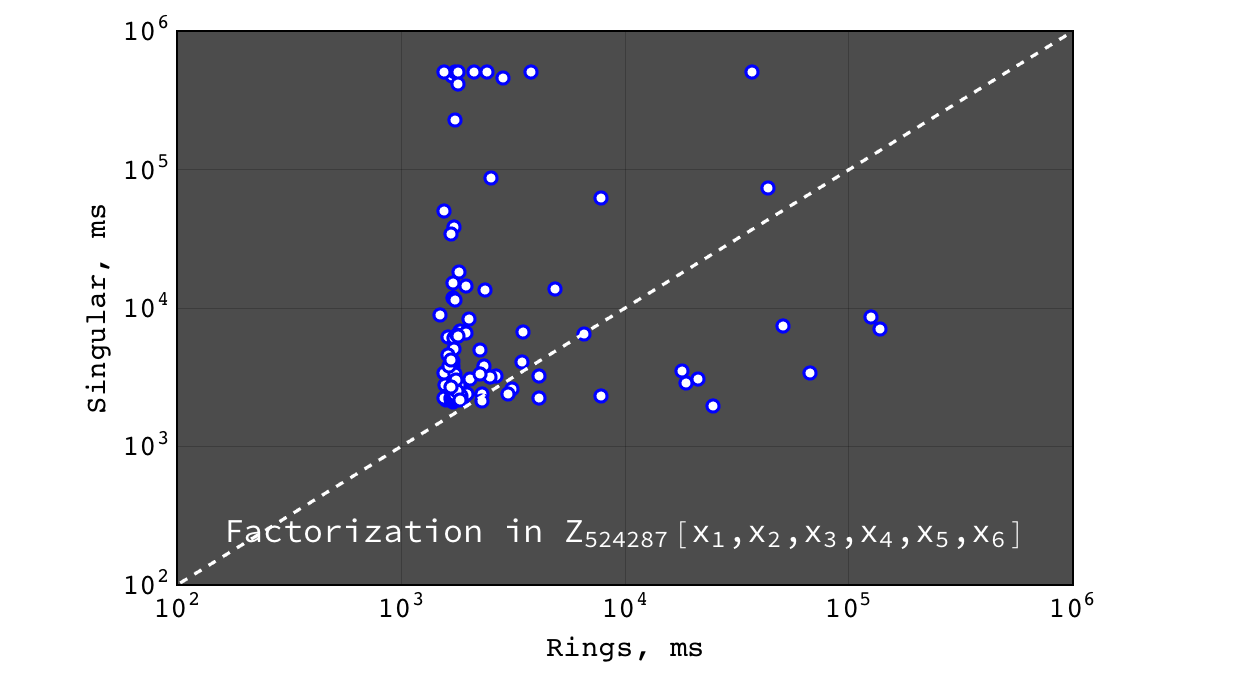
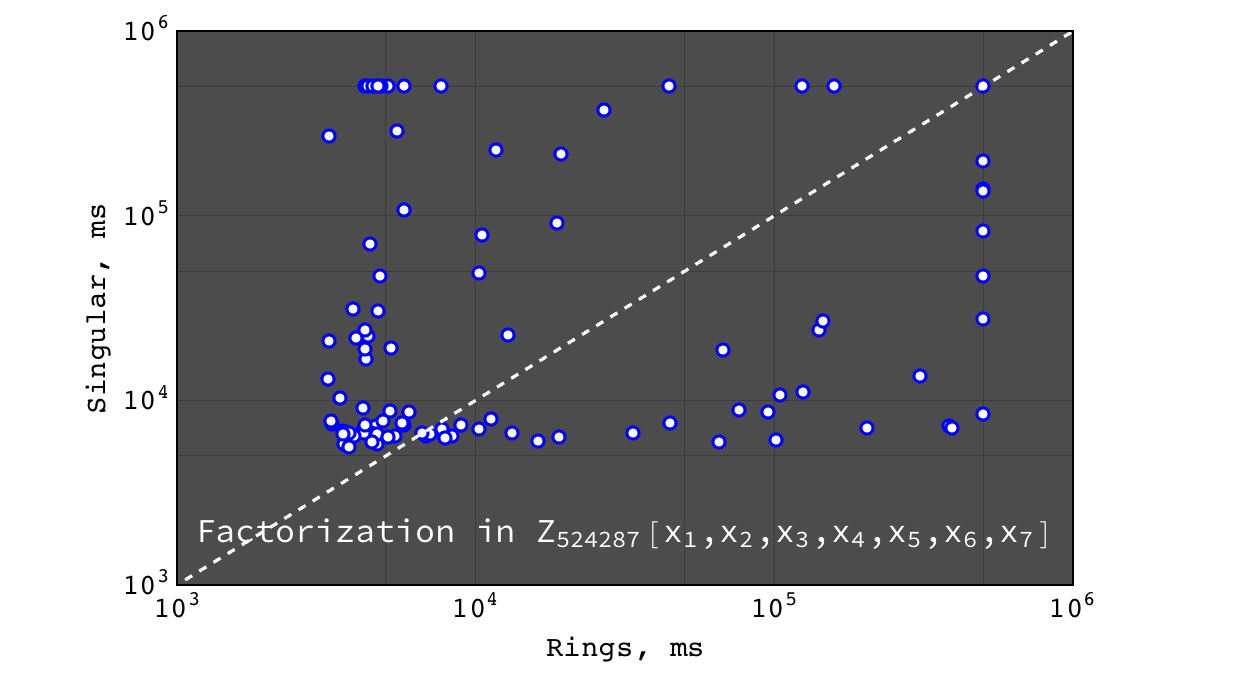
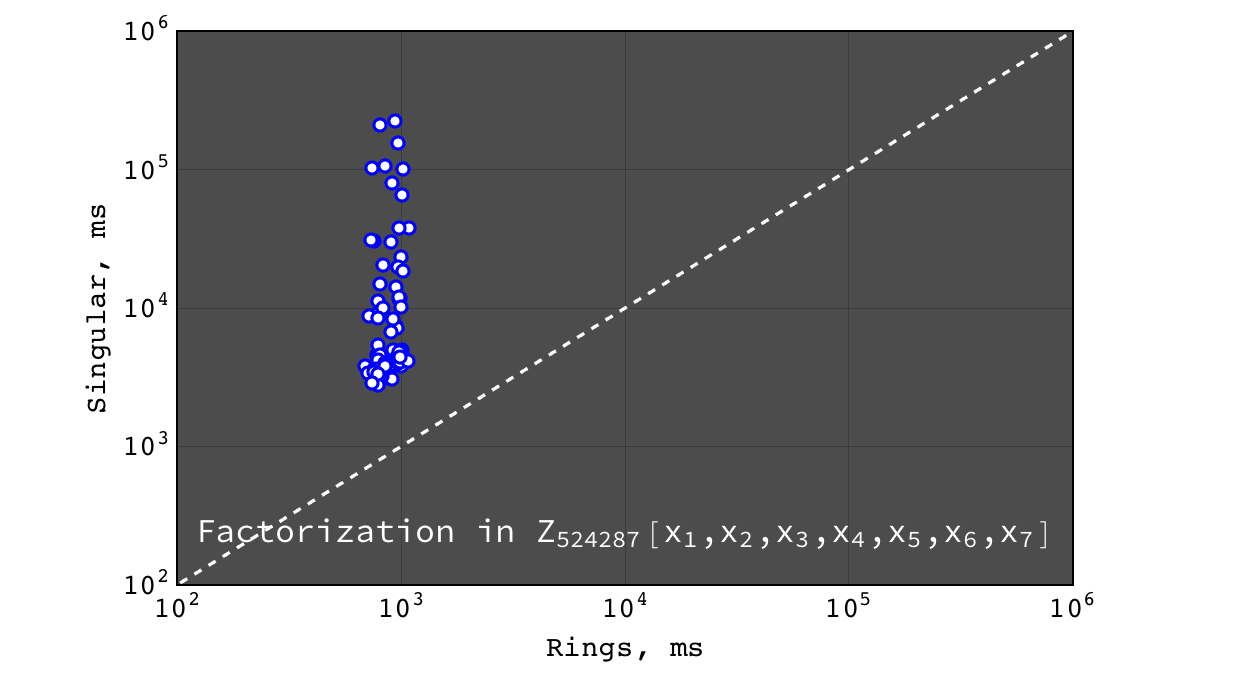
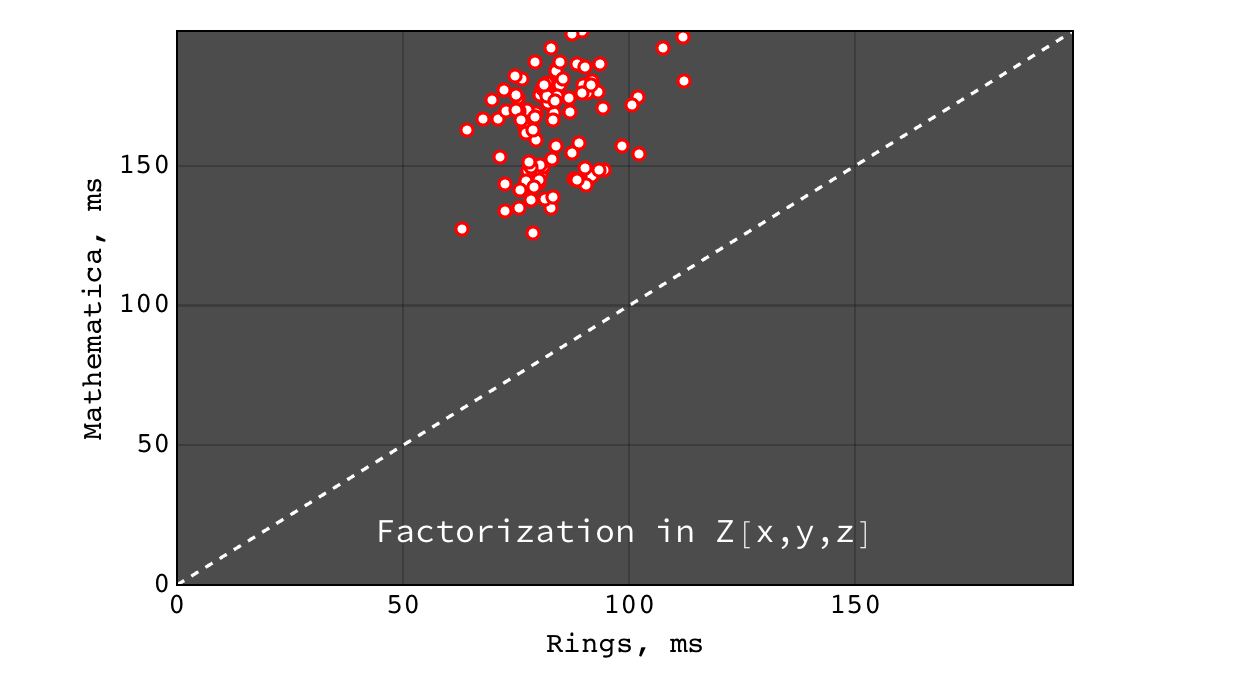
Multivariate factorization¶
Multivariate factorization performance was tested on random polynomials in the following way. Three polynomials \(a\), \(b\) and \(c\) with 20 terms and degree 10 in each variable were generated at random. Then the factorizations of \((a b c)\) (should give at least three factors) and \((a b c + 1)\) (usually irreducible) were calculated. So the input polynomials had about ~8000 terms and degree 30 in each variable (so the total degree of input was \(30 * n\), where \(n\) is the number of variables). Tests were performed for polynomials in 3, 4, 5, 6 and 7 variables over \(Z\), \(Z_2\) and \(Z_{524287}\) ground rings.
Brief conclusion
- Rings and Singular are comparably fast and Mathematica is hopelessly slow
- for irreducible polynomials Rings are considerably faster than Singular
- Rings perform better on dense problems
Multivariate factorization over \(Z_2\)¶
These tests were performed for Rings and Singular since Mathematica does not support multivariate factorization in finite fields.
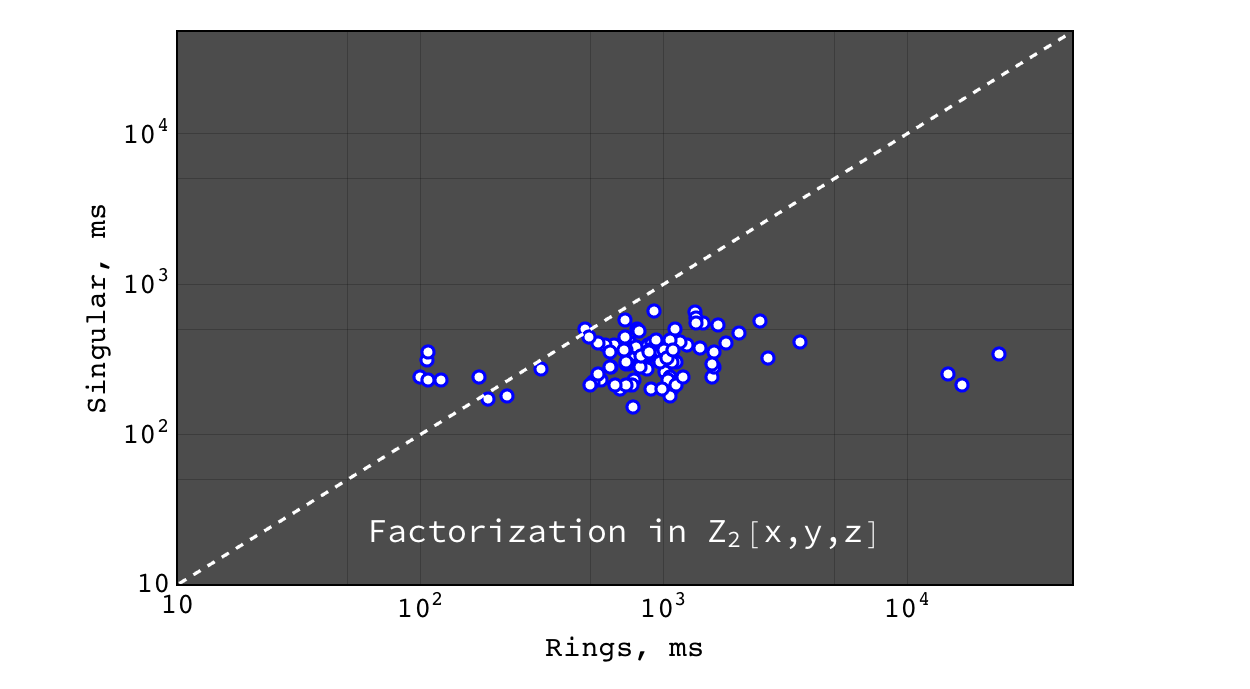
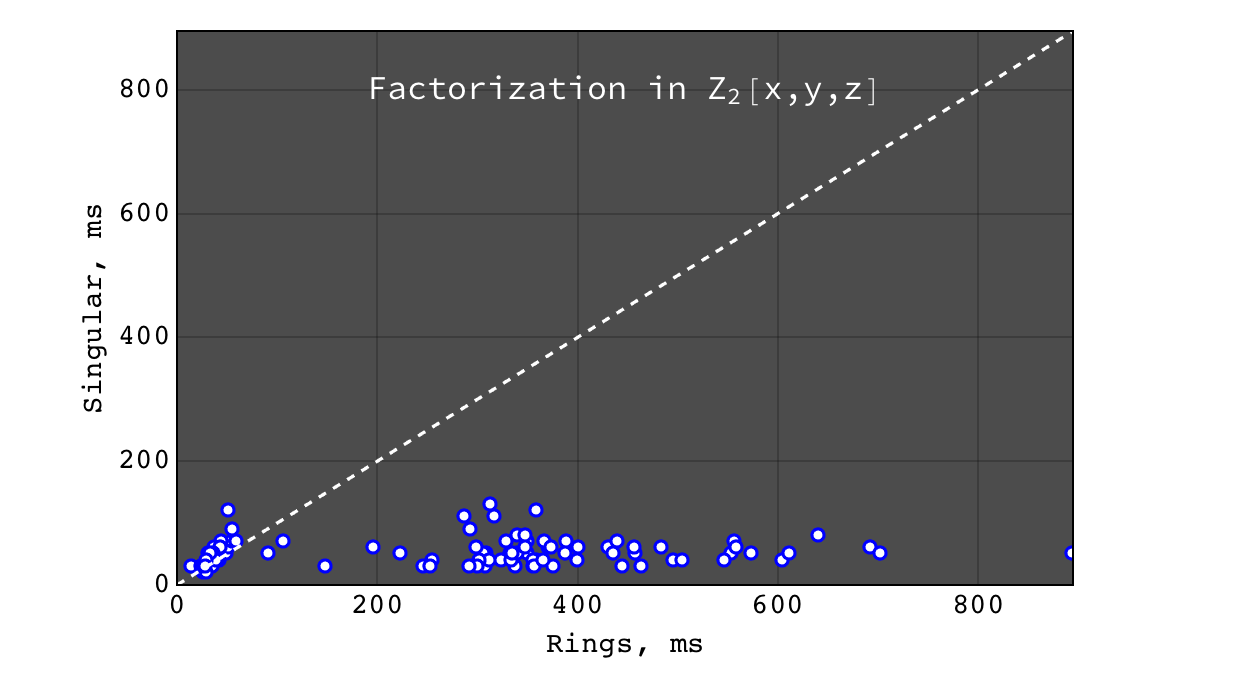
Factorization in \(Z_2[x,y,z]\)¶
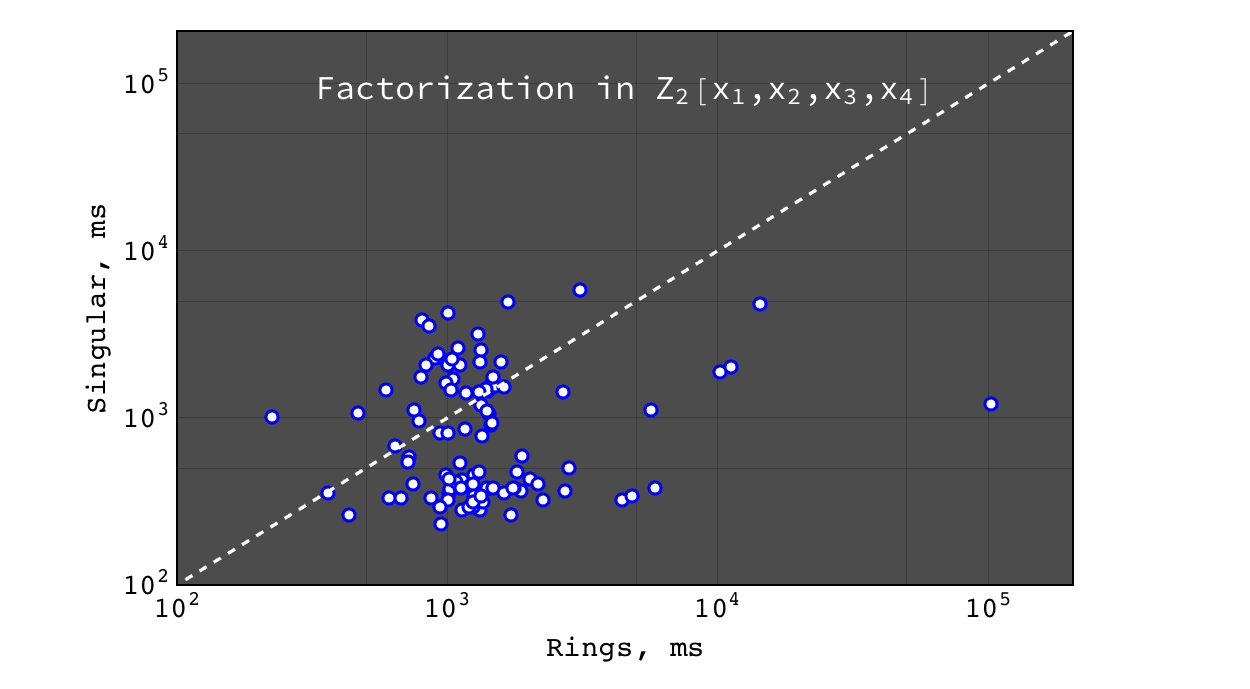
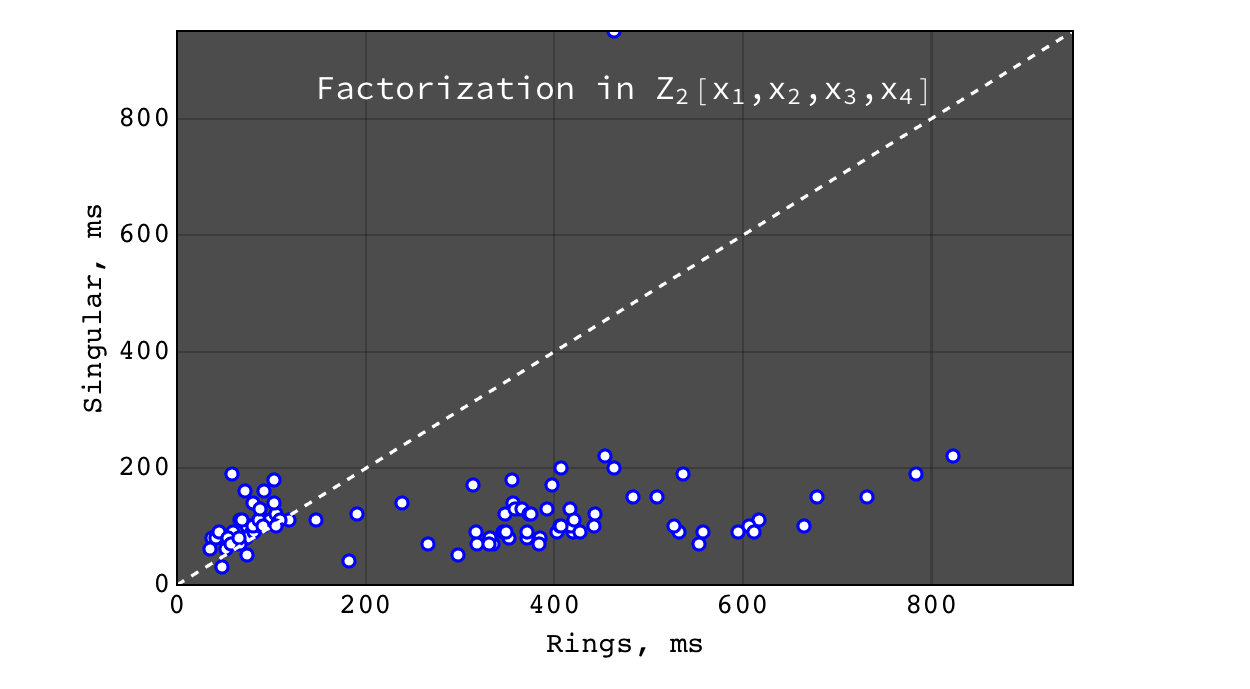
Factorization in \(Z_2[x_1,x_2,x_3,x_4]\)¶
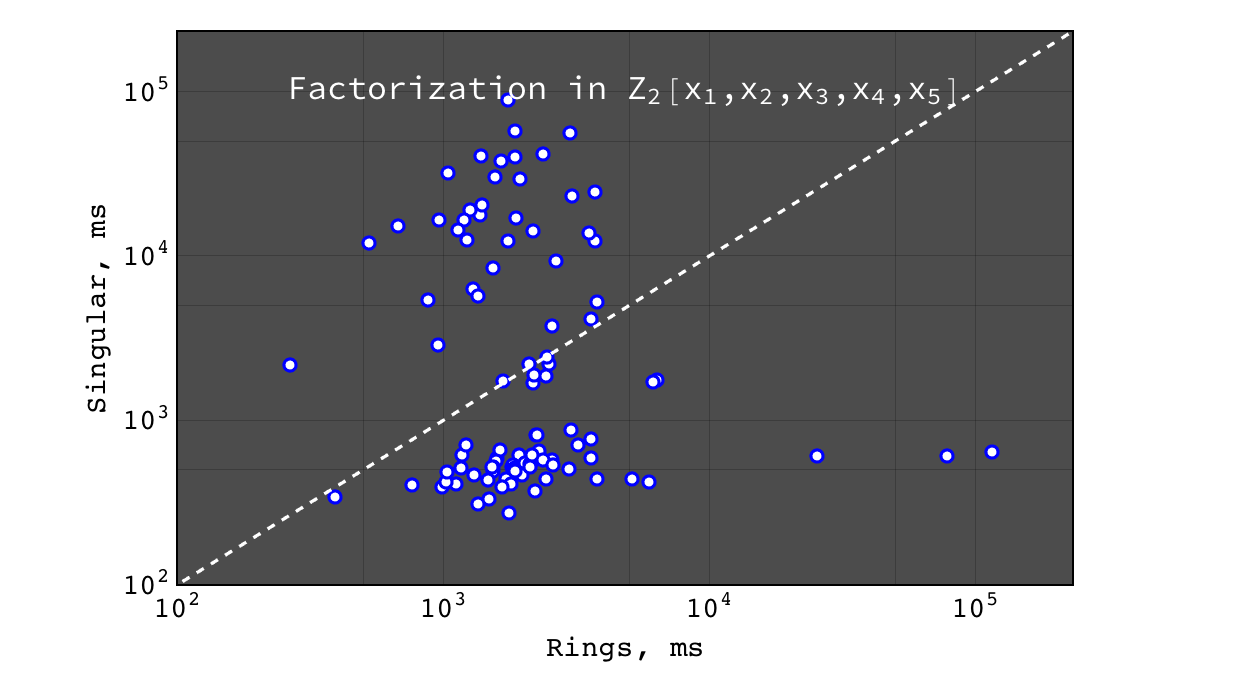
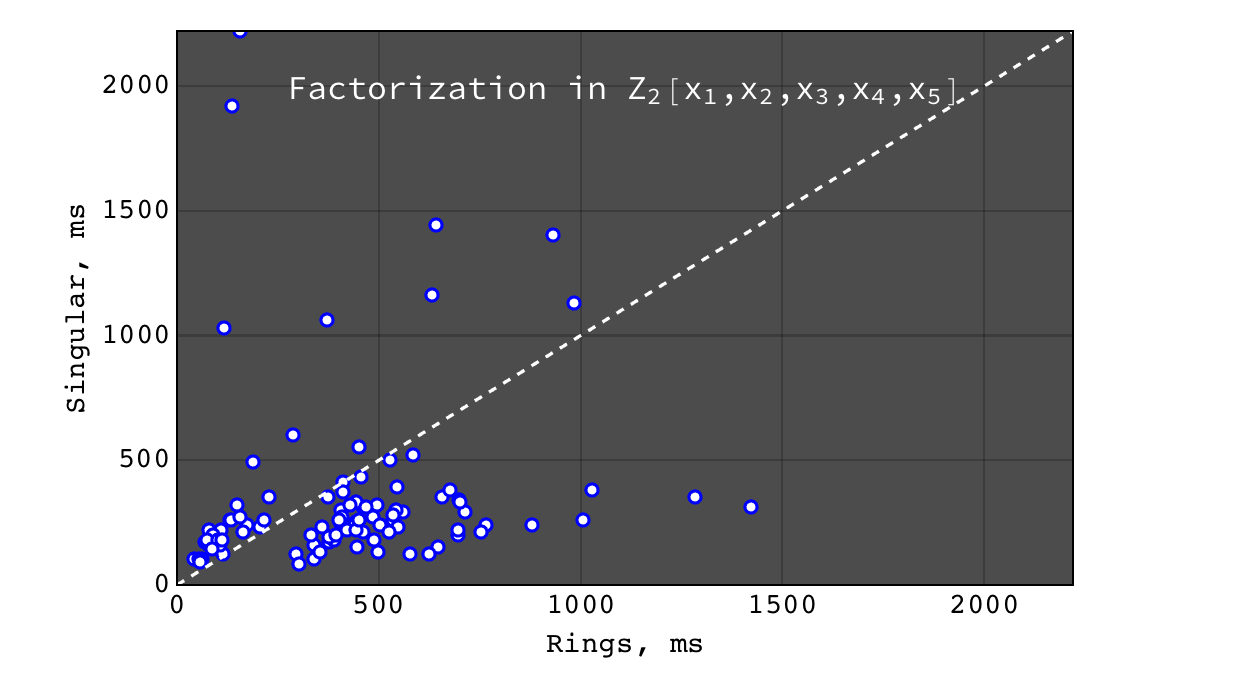
Factorization in \(Z_2[x_1,x_2,x_3,x_4,x_5]\)¶
Factorization in \(Z_2[x_1,x_2,x_3,x_4,x_5,x_6]\)¶
Factorization in \(Z_2[x_1,x_2,x_3,x_4,x_5,x_6,x_7]\)¶
Multivariate factorization over \(Z_{524287}\)¶
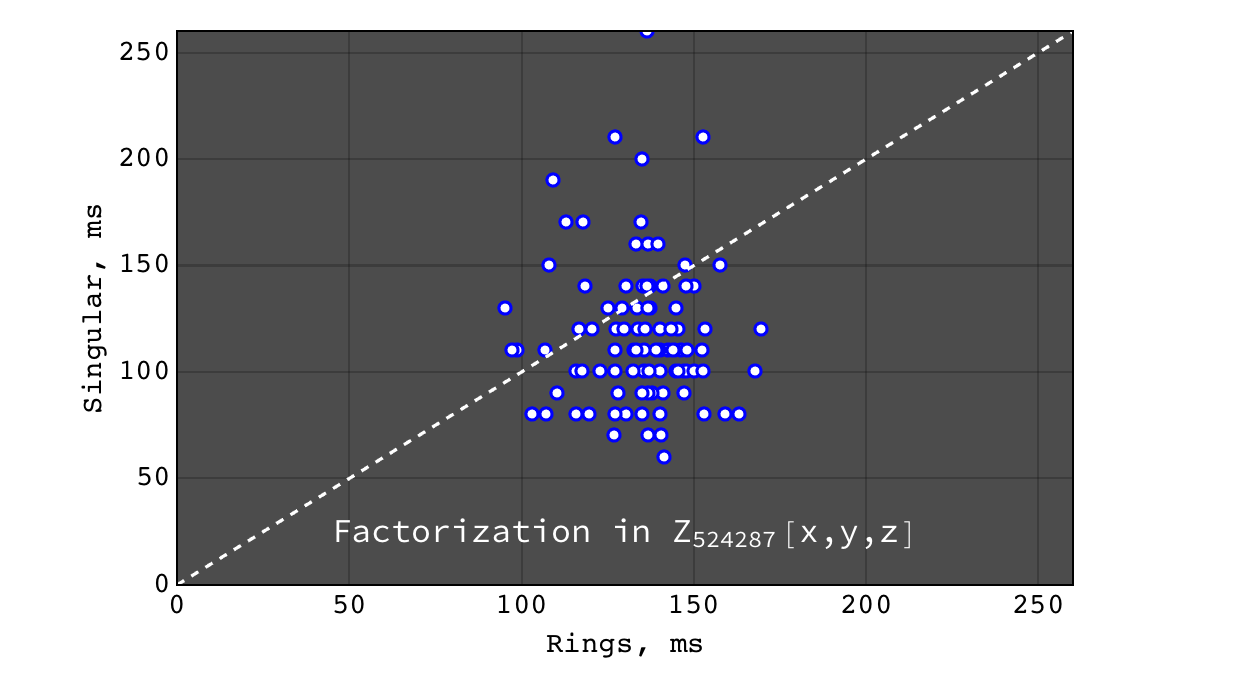
Factorization in \(Z_{524287}[x,y,z]\)¶
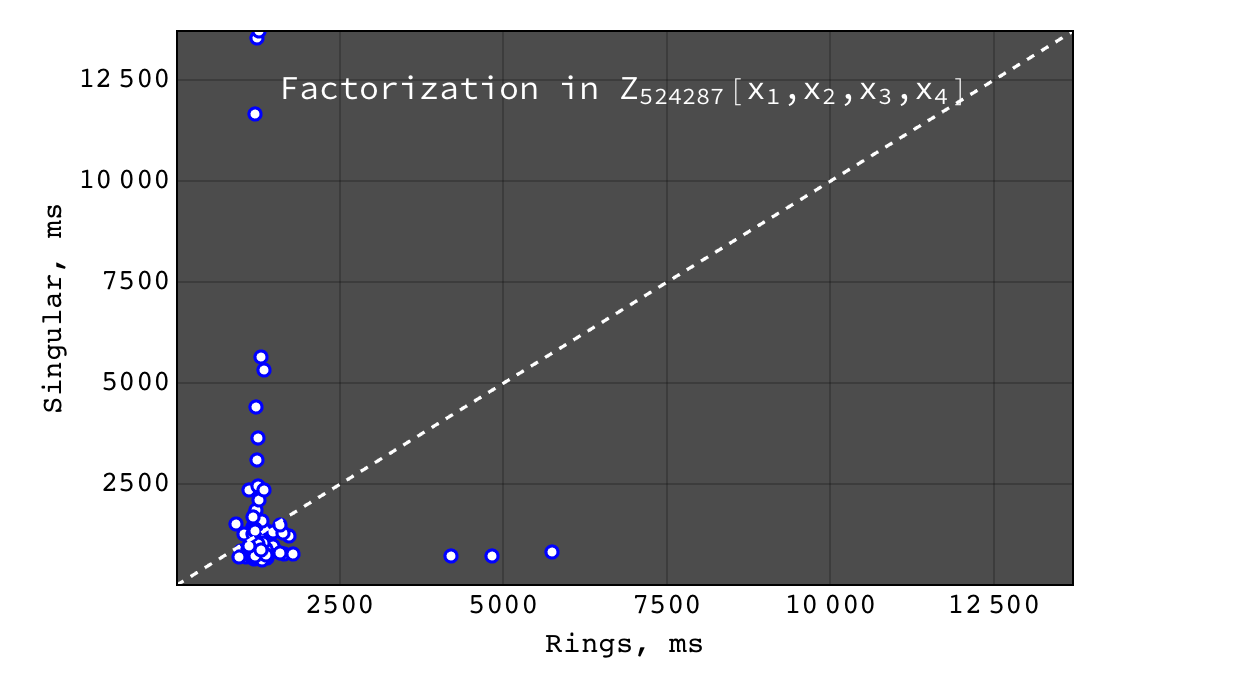
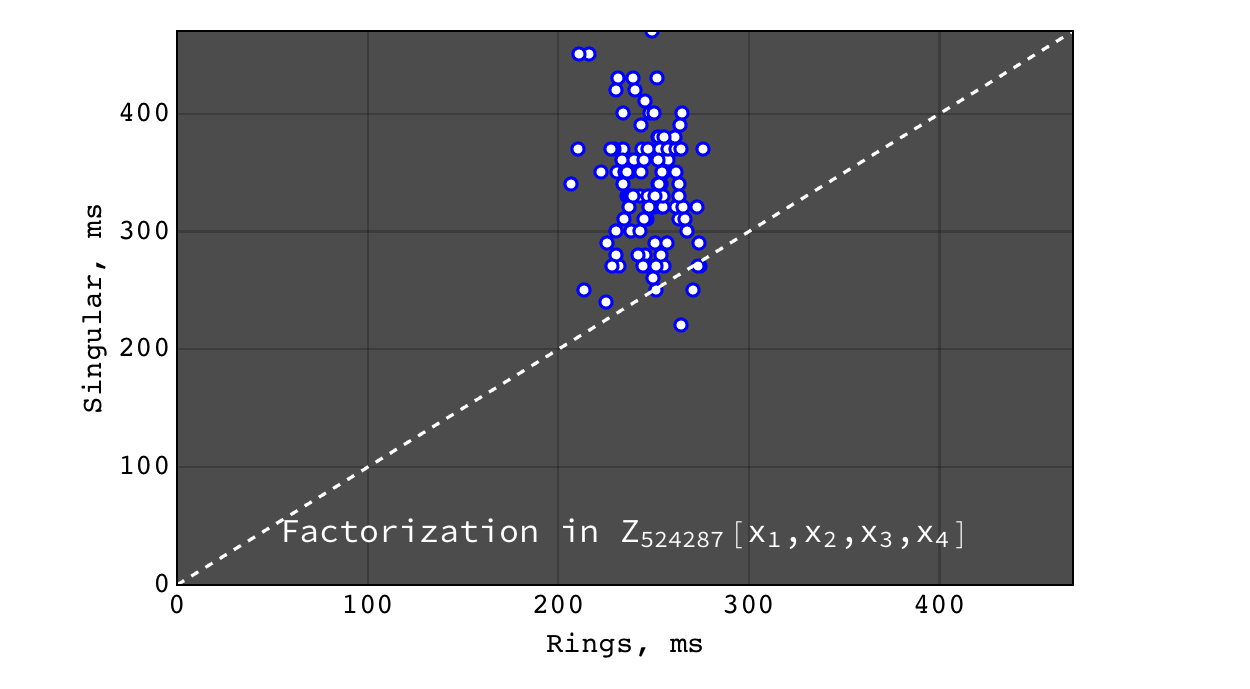
Factorization in \(Z_{524287}[x_1,x_2,x_3,x_4]\)¶
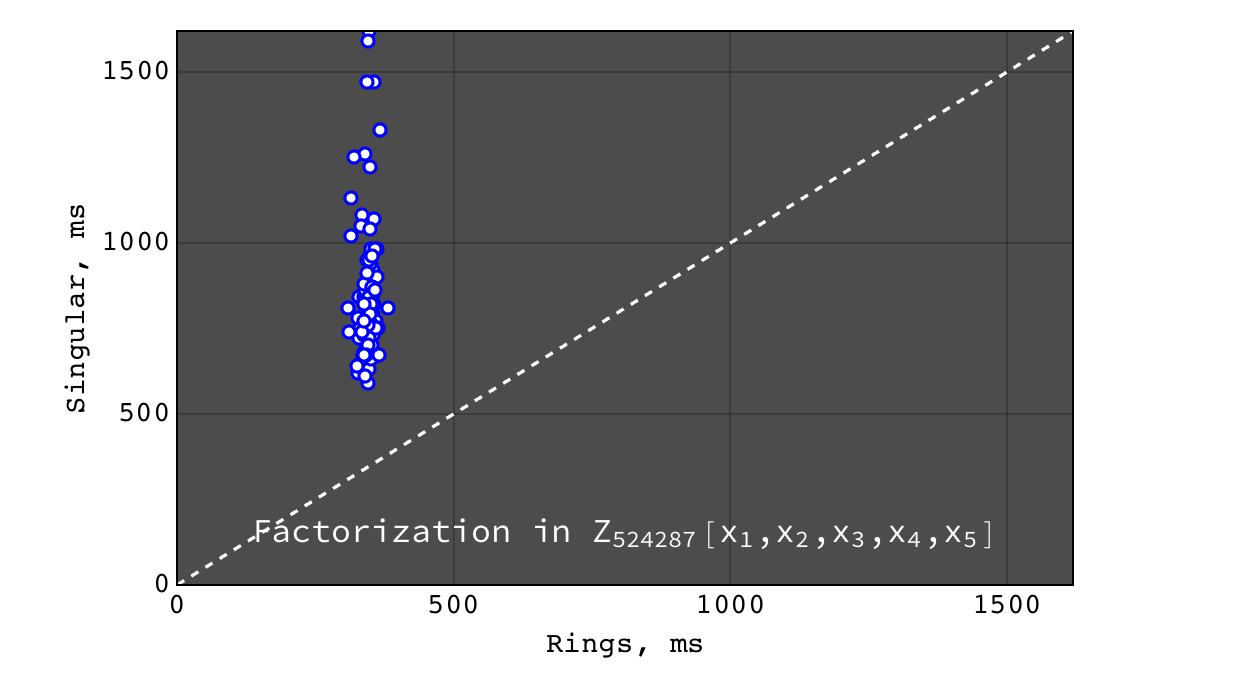
Factorization in \(Z_{524287}[x_1,x_2,x_3,x_4,x_5]\)¶
Factorization in \(Z_{524287}[x_1,x_2,x_3,x_4,x_5,x_6]\)¶
Factorization in \(Z_{524287}[x_1,x_2,x_3,x_4,x_5,x_6,x_7]\)¶
Multivariate factorization over \(Z\)¶
Factorization in \(Z[x,y,z]\)¶


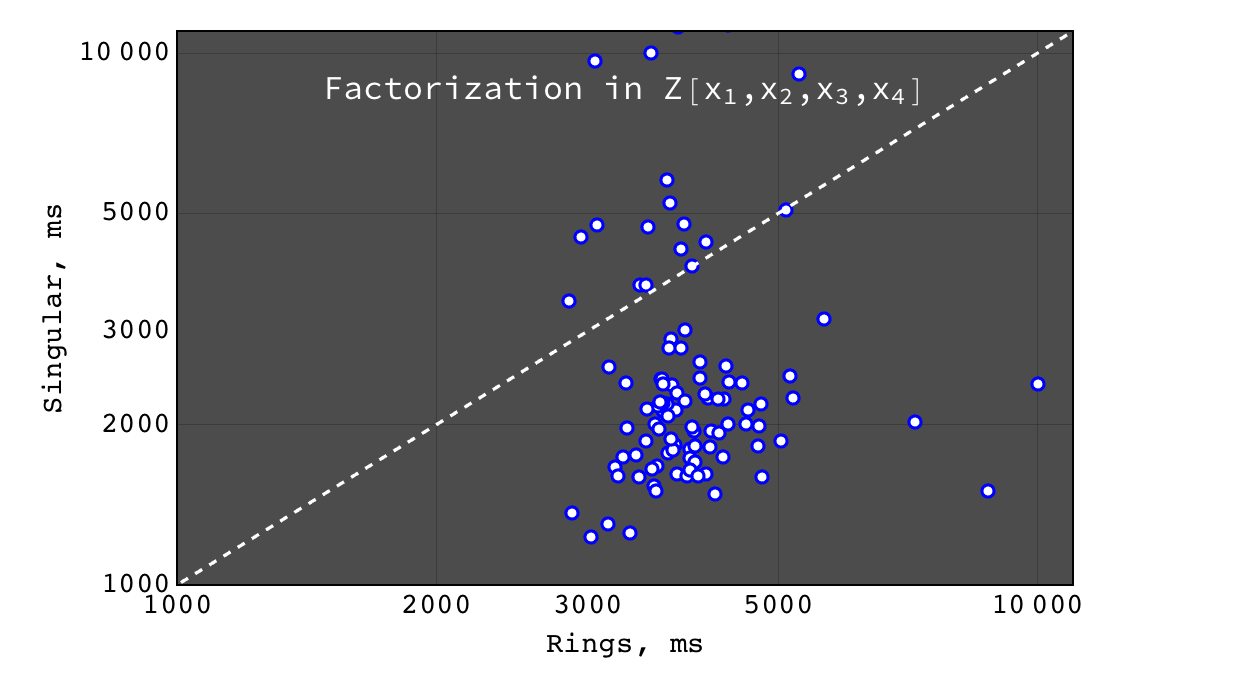
Factorization in \(Z[x_1,x_2,x_3,x_4]\)¶
For non-trivial factorization problems, Mathematica failed to obtain result in a reasonable time, so it is not shown here.
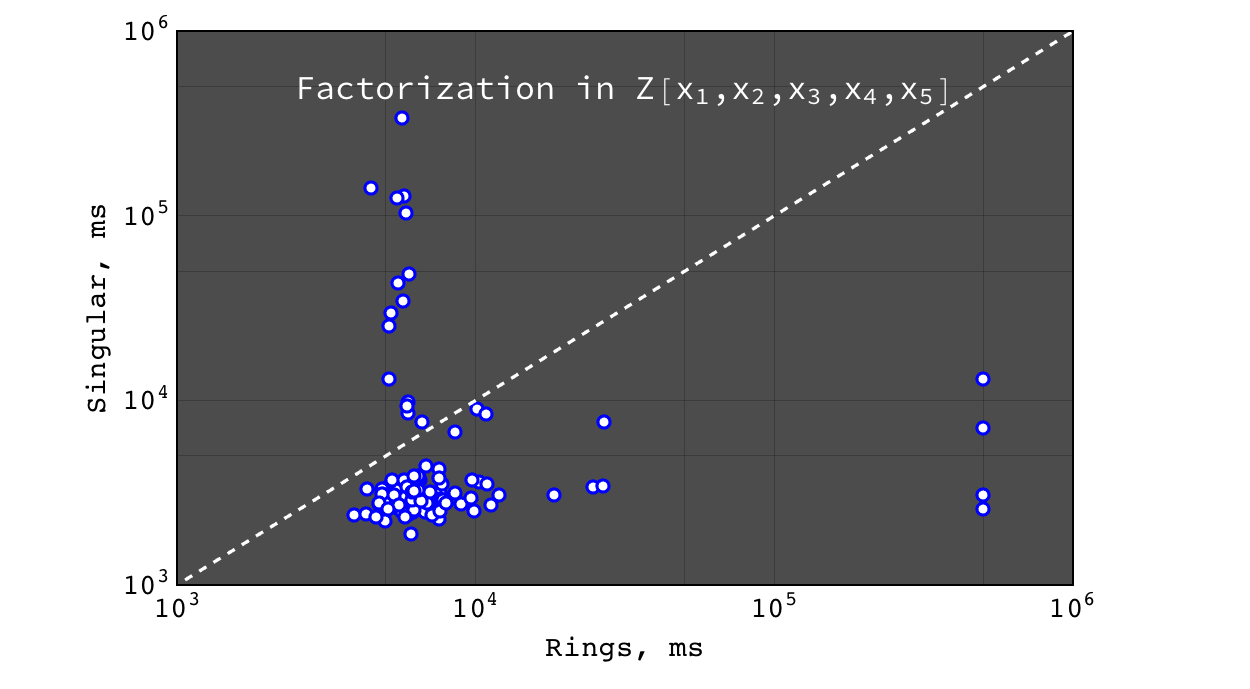
Factorization in \(Z[x_1,x_2,x_3,x_4,x_5]\)¶
Mathematica failed to obtain result in a reasonable time, so it is not shown here.
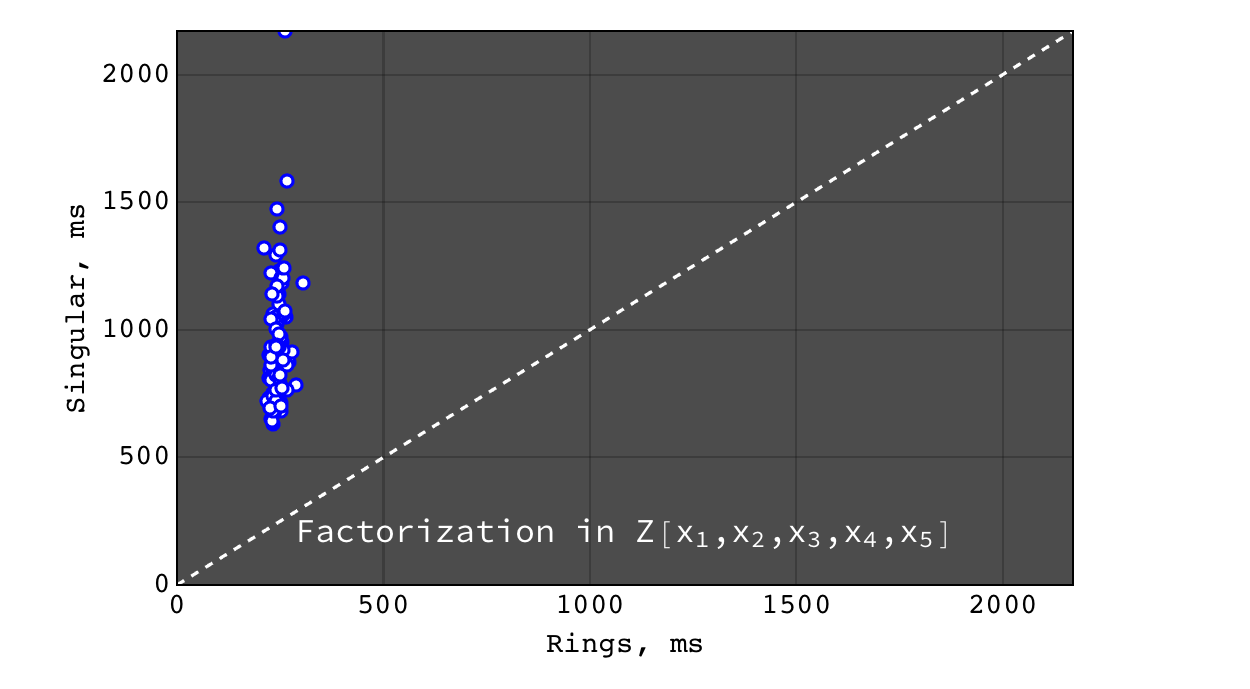
Factorization in \(Z[x_1,x_2,x_3,x_4,x_5,x_6]\)¶
Mathematica failed to obtain result in a reasonable time, so it is not shown here.
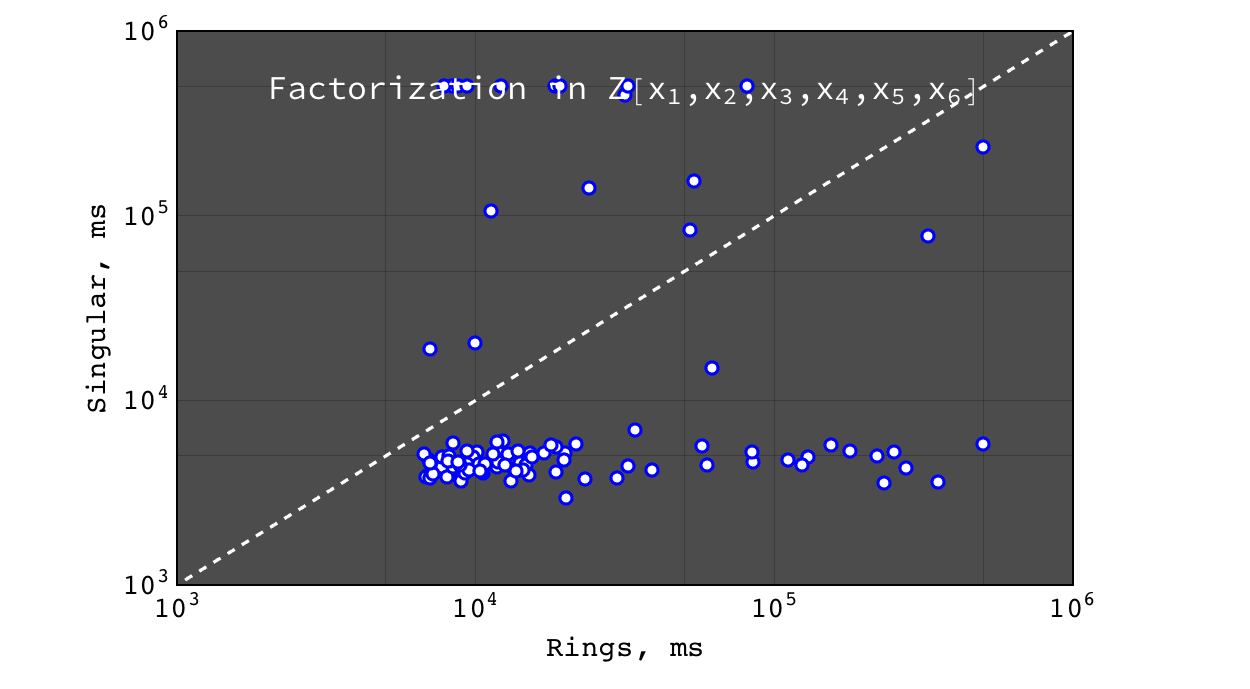
Factorization in \(Z[x_1,x_2,x_3,x_4,x_5,x_6,x_7]\)¶
Mathematica failed to obtain result in a reasonable time, so it is not shown here.
Multivariate factorization on large not very sparse polynomials¶
To check how the above plots obtained with random polynomials scale to a really huge and more dense input, the following factorizations were tested.
Factor
over \(Z\), \(Z_2\) and \(Z_{524287}\) coefficient rings:
| Coefficient ring | Rings | Singular | Mathematica |
|---|---|---|---|
| \(Z\) | 55s | 20s | 271s |
| \(Z_2\) | 250ms | > 1 hour | N/A |
| \(Z_{524287}\) | 28s | 109s | N/A |
Factor
over \(Z\), \(Z_2\) and \(Z_{524287}\) coefficient rings:
| Coefficient ring | Rings | Singular | Mathematica |
|---|---|---|---|
| \(Z\) | 23s | 12s | 206s |
| \(Z_2\) | 6s | 3s | N/A |
| \(Z_{524287}\) | 26s | 9s | N/A |
Univariate factorization¶
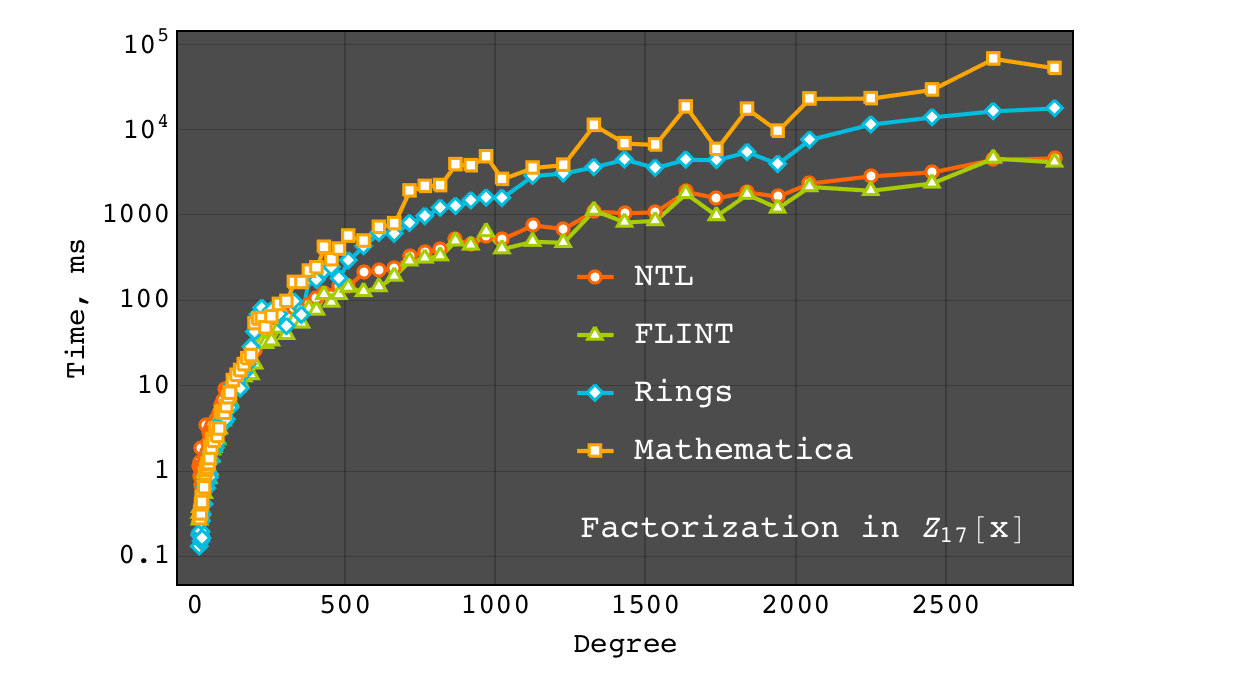
Performance of univariate factorization was compared to NTL, FLINT and Mathematica. Polynomials in \(Z_{17}[x]\) of the form:
were used.
At small degrees the performance is identical, while at large degrees NTL and FLINT have much better asymptotic, probably due to more advanced algorithms for polynomial multiplication.